Постановка проблемы. Как решать простейшее
диофантово уравнение вида ax +
bx = 1? Оказывается разложение числа a / b в непрерывную дробь даёт путь к решению.
Достаточно рассмотреть числитель и знаменатель предпоследней
подходящей дроби, подобрав знаки. |
Цели работы. Познакомиться
с алгоритмом построения подходящих дробей, который лежит в основе
эффективного нахождения целых решений уравнения ax
+ bx = 1 (a и b целые). |
Теорема (без доказательства). Числители и знаменатели подходящих дробей
удовлетворяют одному и тому же простому рекуррентному соотношению:
Pn+1 = Pn * an+1 + Pn-1
где Pn обозначают числитель (или знаменатель,
если вычисляются знаменатели) n-ой
подходящей дроби), а an+1 - (n+1) - ый член
непрерывной дроби. |
| Пример. Рассмотрим построенную ранее
непрерывную дробь для рационального числа 3367/1001: |
Числитель |
Знаменатель |
Деление нацело |
Построение
непрерывной дроби |
3367 |
1001 |
3367 = 1001×3 + 364 |
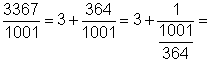
|
364 |
1001 |
1001 =364 ×2 + 273 |
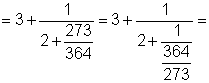
|
364 |
273 |
364 = 273 ×1 + 91 |
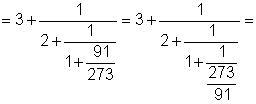
|
91 |
273 |
273 = 91×3 + 0 |
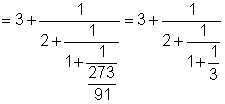
|
|
| Построим по теореме подходящие дроби: |
Пример. Построение подходящих дробей.
Номер: n |
-1 |
0 |
1 |
2 |
3 |
4 |
Члены непрерывной дроби an |
|
|
3 |
2 |
1 |
3 |
Числитель подходящей дроби Pn |
0 |
1 |
3 |
7 |
10 |
37 |
Знаменатель подходящей дроби Qn |
1 |
0 |
1 |
2 |
3 |
11 |
|
Комментарий к
примеру. Непрерывная дробь для
числа 3367 / 1001 имеет следующие члены: 3, 2, 1. 3. Они выписаны во второй строке (номера
над ними). Первые две подходящих дроби 3 / 1
и 7 / 2 можно подсчитать устно. Далее применяем
рекуррентную формулу. Например, число 37 получается комбинацией
чисел находящихся в подсвеченных клетках. Для того, чтобы считать
первые две подходящие дроби по той же формуле, можно добавить две
фиктивные подходящие дроби с номерами 0
и -1
(правильнее сказать, что это просто пары чисел, а не дроби, так как
деление на 0
не определено), которые всегда одинаковы (в таблице они находятся в
затемнённых клетках).
Обратите внимание, что
последняя подходящая дробь совпадает с исходным числом: 37 / 11 = 3367 / 1001,
только сокращена! Этим пользуются в вычислительных алгоритмах для
сокращения дробей, так как сокращение через разложение на множители
требует для больших чисел существенно большего объёма работ. |
Задание 1*. (на
межпредметные связи с информатикой). Напишите на знакомом вам
алгоритмическом языке изложенный выше алгоритм сокращения дроби. |
| |
Теорема (без доказательства). Если числа a и b взаимно просты, то решение уравнения ax + by = 1
может быть получено следующим образом:
- разложить число a/b в
непрерывную дробь,
- взять в качестве x знаменатель,
а в качестве y числитель предпоследней подходящей дроби,
подобрав им нужные знаки. |
| Пример. Уравнение 37x + 11y = 1 имеет решение x = 3, y = -10 (для того, чтобы
определить знак, достаточно посчитать последнюю цифру каждого из
слагаемых). |
Задание 2. Решите диофантово уравнение 64x + 49y = 1.
1. Разложите дробь 64 / 49 в
непрерывную используя инструмент в таблице слева.
2. Постройте числители подходящих дробей, используя
инструмент в таблице справа (во второй столбик нужно поместить
члены подходящей дроби). Проверьте правильность: последний
числитель должен быть равен числителю исходной дроби, то есть 64.
Запишите предпоследний числитель.
3. Постройте знаменатели подходящих дробей,
используя инструмент в таблице справа (второй столбик, в котором
находятся члены подходящей дроби, менять не надо). Аналогично
проверьте правильность и запишите предпоследний знаменатель.
4. Используя записанные числа, подберите знаки и
проверьте, что получилось решение исходного диофантова
уравнения. |
|
| Задание 3. Используя встроенные в страницу
инструменты, сократите дробь 8249 / 7081.
Задание 4*. Найдите другие решения добавляя или
вычитая из найденных b (для x) и a (для
y).
Попробуйте написать общую формулу решений.
Задание 5**. Попробуйте исследовать общий случай
решения уравнения ax + by = c
в целых числах, и определив при каких условиях на a, b и c решение будет существовать. Постройте алгоритм
решения. Превратите его в программу. |
| Работы учеников. |