Постановка
проблемы. Свойства
логарифма позволяют быстро подсчитывать количество цифр в натуральном
числе, вне зависимости от того, в какой системе оно представлено. С
помощью формулы перехода к другому основанию можно быстро оценить,
во сколько раз изменится число цифр в числе при переводе его из
одной системы счисления в другую. |
Пример. Все
трёхзначные натуральные числа заключены в пределах от 100
(включительно) до 1000 (исключая последнее).
lg 100 = 2, lg 1000 = 3. Если 100 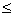 a < 1000, то lg 100 a < 1000, то lg 100 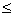 lg a < lg 1000,
т.е. 2 lg a < lg 1000,
т.е. 2 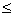 lg a < 3, а это значит,
что логарифм трёхзначного числа начинается с двойки: 2,.... lg a < 3, а это значит,
что логарифм трёхзначного числа начинается с двойки: 2,....
Вычислив целую часть логарифма трёхзначного числа и добавив к результату единицу, мы получим 3, то есть количество его цифр. |
В
общем случае, n-значное
число удовлетворяет неравенствам: lg 10n-1 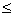 lg a < lg 10n,
т.е. n-1 lg a < lg 10n,
т.е. n-1 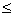 lg a <n, и целая часть a будет равна n-1,
то есть на 1
меньше количества цифр. lg a <n, и целая часть a будет равна n-1,
то есть на 1
меньше количества цифр. |
Определение. Целой частью числа a называется ближайшее целое слева, то есть целое, не
превышающее число a.
Целая часть числа a обозначается [a]. |
|
|
| Выше нами фактически была доказана следующая теорема. |
Теорема. Количество
цифр десятичной записи натурального числа равно 1
+ [lg a]. |
| Перейдём к выполнению заданий. |
Задание 1.
С помощью инструмента вычисления
логарифма вычислите десятичные логарифмы следующих чисел:
1, 12, 123, ..., 1234567890123456789012345. Для этого достаточно ввести основание десятичного логарифма, а затем
вводить по одной цифре числа и наблюдать за результатом. Устно
определяйте целую часть результата и сравнивайте с числом введённых
цифр.
В качестве второго эксперимента можете вычислить логарифмы
чисел, получаемых чтением "с конца": 5, 54, 543,..., 5432109876543210987654321. |
|
| Прежде, чем перейти к следующему заданию, напомним определение позиционной
записи числа. |
Определение. Представлением числа в p-ичной
системе счисления называется его запись в виде:
an pn + an-1 pn-1 + ... + a1 p + a0, где an ,...,a0 называются цифрами числа.
Цифры p-ичной записи числа обязаны
удовлетворять неравенствам: 0 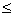 ai < p. ai < p. |
| |
Задание 2.
а) С помощью инструмента перевода чисел из одной системы
счисления в другую переведите в троичную систему числа: 1, 12, 123, ..., 1234567890. Подсчитайте и запишите количество цифр в троичной записи этих
чисел.
б) С помощью инструмента вычисления логарифма вычислите логарифмы
чисел 1, 12, 123, ..., 1234567890 по основанию три. Вычислите целую часть результатов (устно) и
запишите.
в) Сформулируйте гипотезу о вычислении количества цифр натурального
числа в троичной системе счисления. |
|
| Замечание. Перевод числа в троичную систему и вычисление троичного
логарифма можно делать параллельно. Число можно переносить копированием из окна
одного инструмента в другой. |
| Перейдём к теоретическому обоснованию
гипотезы. Предварительно выполните следующее задание. |
Задание
3.
а) С помощью следующих инструментов вычислите степени тройки с
показателями от 7 до 16 (по определению логарифма троичные
логарифмы от полученных чисел будут равны этим показателям
соответственно, можете проверить это с помощью инструмента
вычисления логарифма).
б) Переведите (устно) все полученные
степени в троичную систему (ответ можете проверить с помощью
инструмента перевода). Сколько цифр будут иметь эти числа в троичной системе? |
|
Задание
4*.
а) По определению троичной системе запишите самое маленькое и
самое большое 6-значное число.
б) Обобщите результат,
записав самое маленькое и самое большое n-значное
число в троичной системе счисления.
в)* Сформулируйте и докажите
(по аналогии с приведённым выше доказательством) теорему о выражении
количества цифр в троичной записи натурального числа через троичный
логарифм.
Сравним количества цифр в представлениях
одного числа в разных системах счисления.
Задание 5**.
а)
Сравните количества цифр в десятичной и троичной системах счисления
чисел 1, 12, 123, ..., 1234567890.
Сформулируйте гипотезу о связи между ними.
б) Вычислите логарифм числа 10 по основанию 3.
в)** Напишите формулу перехода логарифма по основанию 3 к
десятичному логарифму. Используя выведенные выше формулы про выражения
количества цифр в числе через десятичный логарифм, напишите формулу,
позволяющую определить во сколько раз изменится число цифр в записи
натурального числа при изменении основания системы счисления.
г) Вычислите логарифмы числа 1234567 по
основанию 10 и по основанию 3. Вычислите логарифм 10 по
основанию 3. Проверьте, что большее из этих трёх чисел
получаются умножением меньших. |
Замечание. Результат вычисления
можно "перетащить" мышкой и вставить в нужное окно (предварительно
выделив число мышкой). |
Работы учеников. |
|
|