|
Постановка
проблемы. В
комбинаторных задачах часто появляется операция вычисления
факториала натурального числа. На практике (например, в теории
вероятности и статистике) часто приходится вычислять n!
приближённо. Для этого нужно суметь найти его
приближённое выражение через известные функции. Этому и посвящена
работа. |
Вычисление
n!
в программе Maxima.
Для вычисления
достаточно набрать нужное число со знаком факториала и нажать
Enter. |
Пример.
(%i1)
10!;
(%o1) 3628800
(%i2)
20!;
(%o2) 2432902008176640000
(%i3)
30!;
(%o3) 265252859812191058636308480000000
(%i4)
40!;
(%o4)
815915283247897734345611269596115894272000000000
В этом примере сначала ввели
10!
и получили ответ
3628800,
затем ввели 20!
и получили
2432902008176640000,
затем ввели 30!
и получили
265252859812191058636308480000000
и т.д. |
|
Проследим за изменением количества
цифр в получаемых результатах:
для 10!
результат имеет
7 цифр, для
20!
– 19
цифр, для 30!
–
33
цифры, для
40!
–
48 цифр, для
50!
–
65
цифр.
Проследим за тем, как увеличивалось
(с каждым десятком)
количество цифр факториала числа.
При переходе от
10!
к 20!
количество цифр увеличилось на
12, при переходе
от 20!
к 30!
- на 14,
далее на 15
и на
17.
|
|
Задание 1. Проследить
за изменением числа цифр в факториалах от
5! до
100! через каждые 5 единиц. |
|
|
|
Задание 2*. Количество цифр можно
вычислять с помощью десятичного алгоритма. Вычислите десятичные логарифмы чисел
полученных в предыдущем задании. Объясните, как по значению десятичного
логарифма определить количество цифр числа. |
|
|
|
Замечание. В
программе Maxima имеются только натуральные
логарифмы: (%i1)
log(10);
(%o1)
2.302585092994046
(%i2)
log(%e);
(%o2) 1
Замечание. В
программе Maxima имеются два режима работы с
подстановкой чисел в выражения. В одном из них число только
подставляется в выражение, во втором происходит вычисление. В
исходном состоянии программа находится во втором режиме, и при
написанных выше действиях получится следующее:
(%i3) log(10);
(%o3) log(10)
Для того, чтобы перейти в
численный режим надо в меню "Численные вычисления" выбрать опцию
"Переключить флаг numer". На экране появится
информация о выполненном переключении:
(%i4)
if numer#false then numer:false else numer:true;
(%o4)
true
Если эту операцию
сделать повторно, программа вернётся в исходное состояние:
(%i5)
if numer#false then numer:false else numer:true;
(%o5)
false
Указание. Для
вычисления десятичных логарифмов нужно
воспользоваться формулой перехода к новому основаниюи определить десятичный логарифм, например, так:
(%i6)
lg(x):=log(x)/log(10);
(%o6) lg(x):=log(x)/log(10)
(%i7)
lg(10);
(%o7) 1
(%i8)
lg(%e);
(%o8) 0.43429448190325 |
Подведём первые итоги.
Если бы
факториал возрастал как показательная функция,
количество цифр изменялось бы (примерно) на одинаковую величину.
Наша же последовательность из приращений числа цифр возрастает.
Значит, факториал растёт быстрее показательной функции.
Сравним рост n!
с ростом nn.
Для этого введем выражение равное отношению
n! и
nn и проследим за его
изменением при росте n.
Как это сделать в программе Maxima показано
на следующем примере (после ввода формулы было сделано переключение
в численный режим). |
(%i9)
R(n):=n!/n^n;
(%o9)
R(n):=
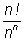
(%i10)
if numer#false then numer:false else numer:true;
(%o10) true
(%i11)
R(10);
(%o11) 3.6288*10-4
(%i12)
R(20);
(%o12) 2.3201961595312499*10-8 |
|
Видно, что nn
растёт быстрее
n!, и что их
отношение убывает как показательная функция (при увеличении
n от
10 до
20 отношение
уменьшилось примерно от 10-4
до
10-8).
Для компенсации умножим отношение на
en и
вычислим значения для n=10 и 20: |
(%i13) S(n):=R(n)*%e^n;
(%o13) S(n):=R(n)*%en
(%i14) S(10);
(%o14) 7.992963907619462
(%i15) S(20);
(%o15)
11.25678423128024 |
|
Видно, что теперь
n! можно
примерно считать равным nne-n.
Однако и это равенство можно улучшить. Попробуйте поделить
S(n) на
квадратный корень из n: |
|
(%i10) T(n):=S(n)/sqrt(n); |
Задание 3.
Вычислите значение выражения для
n = 10, 20, 30,...,100.
Напишите полученную
приближённую формулу для
n!.
Задание 4*.
Найдите в
сети Интернет или учебниках по математике формулу Стирлинга.
Как надо подправить выведенное выше отношение,
чтобы самостоятельно прийти к этой формуле. Найдите
соответствующее отношение
F(n) и
вычислите его значения для
n = 10, 20, 30,...,100.
|
|
Работы учеников.
|