Возьмите два художественных произведения различных авторов с примерно одинаковым
числом страниц (больше 300).
Используя таблицы случайных чисел, выберите в каждом произведении по
60 страниц.
На каждой из выбранных страниц, используя ту же таблицу, выберите строку,
содержащую некоторое предложение или его начало. Таким образом, выбирается
60 предложений, в которых подсчитывается число слов.
Для каждого автора:
1. Постройте полученный ряд чисел.
2. Расположите полученные числа ai
в порядке возрастания на одной координатной оси, а на другой укажите их
частоту
ni (т.е. сколько раз это число
появилось).
3. Соедините точки M(ai
;ni )
отрезками. Получите график частот.
4. Постройте гистограмму частот.
5. Вычислите среднее арифметическое числа слов
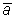 в предложении. в предложении.
6. Вычислите медиану распределения числа слов в предложении.
7. Вычислите разброс (дисперсию) числа данных вокруг среднего арифметического по
формуле
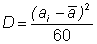
8. Вычислите медиану числовых данных.
10. Разбейте числовой ряд количества букв в предложении на 10 групп.
Если A
– наименьшее число слов , а B
– наибольшее, то в первую группу
войдут те предложения, в которых число слов больше, чем
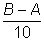 , или равно ему, и не
больше, чем , или равно ему, и не
больше, чем
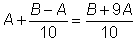 , во вторую – те предложения, в которых число слов больше, чем , во вторую – те предложения, в которых число слов больше, чем
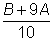 , но
не больше, чем , но
не больше, чем
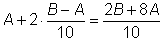 и т. д.
и т. д.
11. Повторите построения пп.1-8, взяв в качестве числа середину интервала.
12. Сравните полученные значения дисперсии для числовых данных до и после
группировки.
13. В каком случае разброс числовых данных оказался меньше?
14. Сравните полученные данные для разных авторов.
Можно проделать ту же работу для произведения ещё одного автора и сравнить
результаты.
|