|
Постановка проблемы. Предложенные
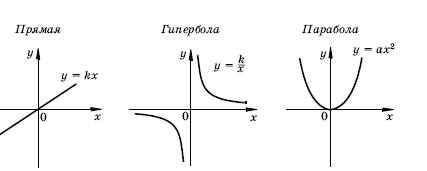
в учебнике простейшие зависимости часто встречаются в описании
различных физических явлений, например, прямолинейного равномерного и
равнопеременного движения. Представляет интерес рассмотреть плоское
движение точки, при котором зависимость каждой координаты (как x,
так и y ) от времени является простейшей. Какую траекторию при
этом будет описывать точка? |
|
|
|
Цели
работы. Нам предстоит:
-
Освоить графические возможности для построения кривых, заданных
параметрически, в программе Maxima.
-
Провести эксперименты с построением кривых, заданных
параметрически и имеющих физический смысл в описании плоского
движения.
-
Научиться работать с областью определения и областью значений.
Вводная
информация.
Для
моделирования кинематики плоского движения (движения точки по
плоскости) нужно задать закон изменения каждой из координат точки от
времени: x = x(t) и y = y(t) и
промежуток времени, на котором рассматривается движение тела.
Следующая
команда позволяет вывести кривую на плоскости, являющуюся траекторией
движения точки по закону x = x(t)
и y = y(t ) на
промежутке времени от a до
b (в
данном примере
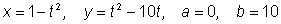 ). ).
|
|
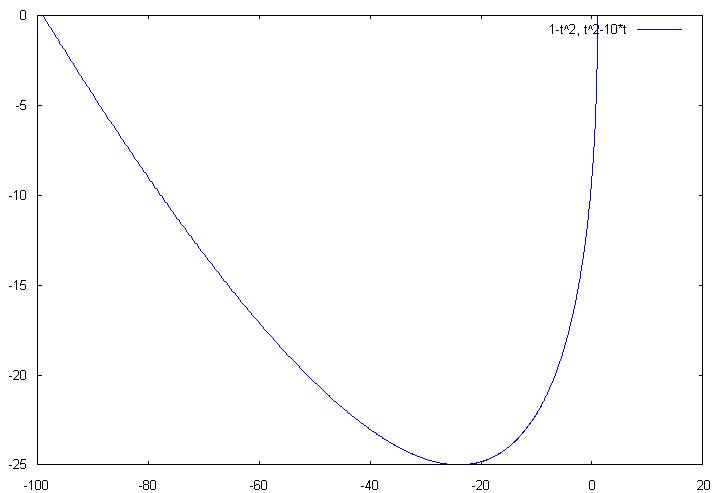
plot2d
([parametric, 1-t^2, t^2-10*t, [t, 0, 10],[nticks, 800]]);
|
|
Первый
параметр этой команды – parametric – указывает на форму задания кривой.
Следующие
два параметра, отделяемыми запятыми определяют выражения x(t)
и y(t). Далее в квадратных скобках указывается имя
параметра и границы его изменения (через запятую). Далее следуют
необязательные параметры, один из которых определяет число точек, по
которым на экране рисуется график (в нашем примере число точек равно
800).
Задания.
|
|
Задание
1. Рассмотрим равномерное движение тела по плоскости.
В этом
случае координаты
x = x(t)
и y = y(t)
задаются
линейными функциями от t.
а) Постройте траекторию плоского движения, если известно, что
координаты меняются по закону
x(t) = 1 – t и y(t) = t, а время движения тела – от t = 0 до t = 1. б)
Задайте закон движения тела таким, чтобы траектория была отрезком,
соединяющим точки
(1;0) и
(0;2)
для того же промежутка времени [0;1].
в)
Задайте закон движения тела таким, чтобы траектория была отрезком,
соединяющим точки
(0;2) и
(3;0)
для того же промежутка времени
[0;1].
Задание
2. Рассмотрим равнопеременное движение тела по плоскости.
В этом
случае координаты x = x(t) и y = y(t) задаются
квадратичными функциями от t. Из
физики мы знаем, что траектория движения в этом случае –
парабола. Однако, в отличие от параболы, которая является графиком
квадратичной функции, это парабола «общего вида». Ось
этой параболы необязательно будет параллельна оси ординат.
Постройте
параболическую траекторию
а) ось симметрии которой совпадает осью абсцисс;
б) вершина которой лежит в первой четверти, а ось не параллельна
координатным осям;
в) ось симметрии которой совпадает с биссектрисой I – III координатных
углов.
|
|
Работы учеников. |
|