Основное назначение данного ИУМК – это разработка современных педагогических и информационно-коммуникационных технологий, рассчитанных на использование как классических методов и подходов к решению методических задач, так и современных подходов.
Классические формы обучения в течение многих лет давали возможность добиваться больших успехов. У каждого конкретного учителя имеется свой педагогический стиль преподавания, своя методика обучения, свое видение последовательности изложения материала. Поэтому новые инструментальные средства должны помочь учителю реализовать свои возможности и устремления новыми (более эффективными и современными) средствами.

Наша задача – помочь учителю, облегчить его работу, но в то же время сделать ее более эффективной, не увеличивая нагрузку на участников учебного процесса, т.е. на учителей и учащихся. Большинство материалов направлено не на автоматизацию и ужесточение контроля с помощью технических средств, а на расширение познавательных инструментов, позволяющих по новому увидеть изучаемый материал, выбрать те формы его представления, которые наиболее "по душе", разобраться в сути математических идей.

Формы контроля чётко выделены - это контрольные работы, подготовленные с помощью генератора типовых заданий, так чтобы у каждого ученика был свой вариант. Контрольные работы подготовлены в печатной форме и имеются на диске (в настоящее время находятся в общем комплекте ученика и учителя, но при передаче ИУМК ученикам должны быть стёрты из ученических копий).

В ИУМК существенно расширен спектр форм учебной деятельности: увеличивается доля самостоятельных работ, учебных исследовательских, лабораторных и других работ. Соответственно этому весь комплект разбит на следующие части:

1) краткий учебник со встроенными динамическими моделями (учебные модули);

2) интерактивные задачники, поддерживающие исследовательскую деятельность на параметрических классах задач, объединяющих в себе традиционные задачи, расширяющих их спектр и использующих эти задачи в новой трактовке;

3) лабораторные работы поддерживают конструктивную и экспериментальную деятельность учеников, вводят в обучение компьютерный инструментарий;

4) исследовательские работы поддерживают инициативную деятельность учеников, инициируют их к чтению книг, поиску информации в сети Интернет, постановке и решению новых задач; результаты работ учеников объединяются вместе как расширение встроенного учебника с помощью движка Wiki-wiki;

5) задачи с виртуальными инструментами - это различного вида тренажёры с обратной связью, позволяющие самостоятельно выполнить ряд упражнений на усвоение новых понятий;

6) индивидуальные домашние задания по теме представляют собой типовые и ключевые для темы задания в печатном виде и выдаются ученикам для повторения материала темы;

7) самостоятельные работы также представлены в печатном варианте, могут использоваться как для проведения летучек, так и на уроках, посвящённых решению задач;

8) тесты для самоконтроля сформулированы в виде утверждений, которые надо оценить (да/нет), предназначены для самоконтроля ученика после чтения соответствующего материала учебника;

В качестве навигации по ИУМК имеются две системы ссылок: тематическая (оглавление) и привязанная к предложенному поурочному планированию (расписание). Поскольку для каждого типа дидактических материалов имеется оглавление в форме гиперссылок, из них можно быстро собрать новый учебный план, копируя ссылки в предложенную форму поурочного планирования (с помощью любого любого редактора HTML-текстов). 

Учебный материал предлагается в двух вариантах: печатном и HTML-формате (и ориентирован на применение движка WIKI-WIKI).
Основная структурная единица – учебный модуль. Он посвящен изучению одного или нескольких тесно связанных между собой понятий.
В печатном варианте выступает как краткий учебник-справочник для поддержки самостоятельной деятельности.
В электронном варианте выступает как базисная часть создаваемого совместно с учениками расширенного учебника.
Весь курс 10 класса делится на 5 глав. К каждой главе предлагается несколько модулей, приближенных по составу к отдельным урокам.
Курс 11 класса делится на 4 главы, и к каждой главе также предлагается несколько модулей.
Большинство модулей включает динамические иллюстрации, модели, инструменты, инициирующие деятельность обучаемого.

Модули, содержащие динамические элементы, можно и рекомендуется использовать также, как задачники на динамических моделях или лабораторные. А именно, работу с динамическими элементами учебных модулей можно в некоторых случаях ставить как цель урока, в этом случае чтение содержания модуля будет мотивироваться выполнением задания.

Другой вариант использования динамических элементов учебника - объяснение материала учителем с использованием  компьютера с проектором или динамической доской. В этом случае модели могут использоваться двояко: во-первых как динамические рисунки при обсуждении, во-вторых как средство организовать обсуждение упражнений. В последнем случае учитель предлагает выполнить несколько заданий, после чего ответы проверяются на манипуляторе.

Использование движка Wiki-wiki при работе с ИУМК

Требования к учителю и ученикам. Все участники процесса обучения в формате Wiki должны знать правила и указания, которыми необходимо руководствоваться для грамотного и эффективного использования этого формата. Обмен результатами работы по данному модулю может обсуждаться в сети Интернет, в школьной сети Интранет, если такая существует, или в классе. Для обсуждения в классе этой работы выделен 1 час в конце каждой темы.

Пример. Модуль 5.1 Переменные и зависимости.
В модуле излагаются сведения справочного характера. Приводятся основные определения, формулы, формулировки важных теорем и т.п. Отсутствуют доказательства, рассуждения, комментарии.
Основная содержательная часть модуля – поставить перед учеником задачу, связанную содержательно с данным модулем, при решении которой ему придется:
1) обмениваться мнениями с другими учащимися;
2) искать информацию в книгах, в Интернете, в справочниках;
3) научиться высказывать гипотезы и проверять их;
4) учиться пользоваться программными материалами, которые имеются в открытом доступе в Интернет;
5) анализировать высказывания других учеников;
6) грамотно излагать свои мысли;
7) самому придумывать задачи и т.д.
 

Предлагаемая задача может быть
1) задачей на доказательство какого-то математического факта, совсем не очевидного;
2) лабораторной работой, при выполнении которой придется самостоятельно ознакомиться с новым программным продуктом;
3) задачей, содержащей парадоксальное утверждение, и т.д.

Пример.
В модуле 5.1. ставятся задачи:
1. Примеры зависимостей. Найдите интересные примеры зависимостей из разных областей знания и их приложений. Дайте их математическое описание и разъясните смысл приведенных зависимостей.
2. Необычное тождество.
Верно ли, что следующее равенство является тождеством?

 

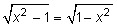
"Тождество – это равенство, верное для всех допустимых значений входящих в него переменных.
В нашем примере допустимые значения для левой части – числа от –1 до 1, а правой – числа больше или равные 1 и меньше или равные -1. Таким образом, допустимыми для обеих частей являются только -1 и +1. Для этих значений обе части уравнения равны 0. Значит, оно является тождеством!
Найдите другие «странные» тождества".

Исследовательскую работу с модулем правильно предложить после того, как соответствующий материал изучен на уроке, выполнены примеры алгоритмического характера, получены некоторые навыки в обращении с новыми понятиями. Время, отведенное для работы с модулем, может варьироваться в пределах от «к следующему занятию» до «к аналогичному занятию на следующей неделе».

Техническое замечание. При открытии вариантов печатных заданий (индивидуальных заданий, самостоятельных работ или контрольных) из браузера автоматически вызывается просмотрщик pdf-файлов (обычно это свободной распространяемый AdobeReader). Возвращение в учебник в этом случае осуществляется средствами браузера -  следует нажать кнопку перехода к предыдущей HTML странице.

Ученик может работать по-разному: спонтанно искать черные линии графика, рискуя получить много красных клякс, или сначала обдумать ситуацию и найти хотя бы одну точку графика аналитическим способом. В любом случае компьютерный карандаш поможет каждому учащемуся справиться с заданием. Ученики могут увидеть взаимное расположение графиков относительно друг друга, так как программой предусмотрена возможность показать на экране график более простой функции. В некоторых манипуляторах этот график появляется при нажатии на клавишу «Показать график». В других манипуляторах вспомогательный график сразу предлагается в качестве подсказки.
 

Проведение урока по преобразованиям графиков функций
В каждой задаче требуется построить график квадратичной функции при различных преобразованиях, например, построить график |f(–x)|.
Изображенный на рисунке график условно разбит на 4 части: 1-й отрезок - в 1-й четверти, 2-й - в 4-й четверти и т.д. При помощи нажатия клавиш каждая часть графика может быть отражена относительно оси OX или оси OY.
Проверка правильности решения задачи осуществляется нажатием кнопки "Проверить". При этом появляется красный или зеленый сигнал «светофора», показывающий, верно ли решена задача, а клавиши для переноса частей графика исчезают. Это исключает возможность подогнать ответ, постоянно наблюдая за «светофором». Нажатие кнопки "Продолжить" позволяет продолжить эксперименты с графиком.
Нажатие кнопок "Показать график"/"Спрятать график" позволяют сравнить полученный график с исходным.

После работы с графиками на компьютере делаются обобщения, обсуждаются свойства функций, графики которых строили ученики, формируются и доказываются правила.

Далее ученикам предлагают задания для самостоятельного построения графика, уже без компьютерного инструмента. Учитель проверяет, у кого возникают затруднения, предлагает еще раз обратиться к компьютеру.

Перед учащимися ставятся четкие вопросы и ведется обсуждение в диалоговой форме. Лучше раздать учащимся опросные листы, листы наблюдений или протоколы урока, куда учащиеся заносят свои наблюдения и делают выводы.
Полезно несколько раз использовать одни и те же манипуляторы и для закрепления знаний, и для обучения самостоятельно анализировать информацию. 

Лабораторные работы выполняются с использованием как специально разработанных программ (апплетов, - например лабораторная работа "Логарифмическая линейка"), либо с использованием программ, входящих в стандартные поставки программного обеспечения для компьютерных классов (например, лабораторная работа "Статистический анализ текста" выполняется с помощью любого стандартного текстового редактора, может использоваться распространенный редактор MS Word, однако он является коммерческим продуктом и может быть заменен аналогичным редактором, входящим в свободно распространяемый OpenOffice). Авторы считают полезным познакомиться со ставшими привычными в работе математиков инструментальными математическими программами. В качестве такой программы выбрана среда Maxima, относящаяся к классу программ с открытым кодом (GNU-лицензия), то есть не просто свободная для использования, но и для дальнейшей разработки. В лабораторных работах с её использованием имеются гиперссылки на сайт, с которого её можно скачать.

Методические рекомендации по работе с программой Maxima

Общие замечания Программа Maxima позволяет вести вычисления с целыми числами и многочленами с целыми коэффициентами неограниченной длины. Это позволяет ввести в математику эксперимент, результаты которого являются не приближёнными, как при численных расчётах, а точными. Возможности программы Maxima намного превосходят потребности школьной программы, поэтому рекомендуется познакомиться лишь с ограниченным числом операций этой программы. На представленном ниже интерфейсе указаны те пункты меню, которые будут использоваться в лабораторных работах. Использование программы Maxima целесообразно: 1) для проведения экспериментальных работ, в которых используются преобразования больших символьных выражений; 2) в качестве справочной системы, позволяющей вывести нужную формулу, вместо того чтобы искать её в традиционном справочнике формул; 3) в качестве средства проверки ответов в задачах алгоритмического стиля; Maxima решает многие стандартные школьные задачи, такие как разложение на множители, упрощение выражений, нахождение корней, построение графиков и т.д., демонстрируя ответ, но не давая решения; 4) для быстрого конструирования задач учителем с получением правильных ответов, например, с её помощью легко придумать новое тождество, построить вариации известной задачи изменением параметров и пр. Начало работы с программой Работа с программой осуществляется посредством ввода выражения (через окно ввода в нижней части интерфейса) и выполнения над ним или его результатами различных команд. Набор команд описывает различные математические операции. Для выполнения команд нужно, чтобы они были правильно записаны. Однако запоминать команды не обязательно, так как для многих из них (практически для всех, что понадобятся в школьном курсе) есть соответствующие им кнопки интерфейса, нажатие которых приводит к вводу соответствующей команды и её выполнению. Рассмотрим пример упрощения выражения по формуле разности квадратов. 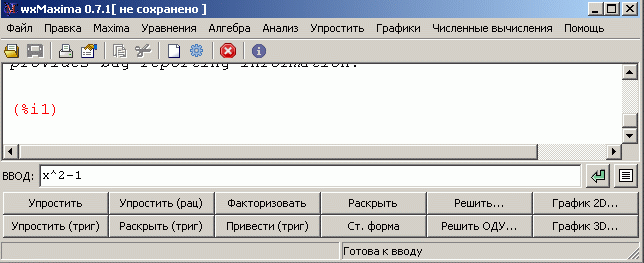Введём выражение в окно ввода, записывая его в строку, как это принято в языках программирования. После нажатия кнопки ВВОД (стрелочка справа от строки ввода) или аналогичной клавиши на клавиатуре (ENTER), выражение будет преобразовано в привычную математическую форму (см. следующий рисунок). 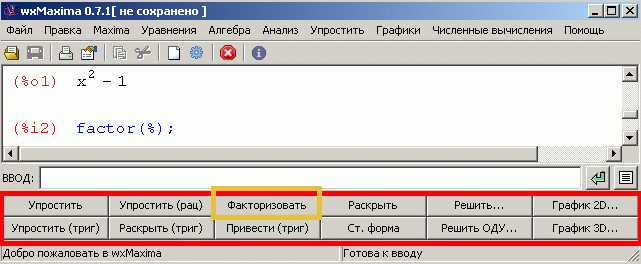Выберем теперь команду ФАКТОРИЗОВАТЬ (так в дословном прочтении с английского именуется команда разложения на множители). Заметим, что к номерам команд добавляется буква "o", когда это результат вычисления (видимо от английского OUTPUT - выход), и буква "i", когда это команда (видимо от английского INSTRUCTION - команда, инструкция). Название команды в данном случае FACTOR, а её аргументом является результат предыдущего действия, что обозначается значком %. 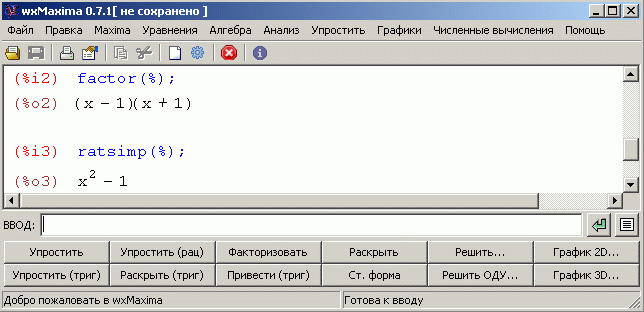Если к результату  (x-1)(x+1)  применить команду УПРОСТИТЬ (которая, как можно видеть на рисунке, именуется RATSIMP), то скобки будут "раскрыты" и получится исходное выражение.   Имена основных математических функций, использующихся при вводе формул возведение в степень: xy   x^y корень квадратный: 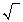  sqrt корень произвольной степени 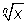записывается степенью с дробным показателем   x^(1/n) экспонента:   ex   exp(x) натуральный логарифм   ln(x)   log(x) логарифм по произвольному основанию 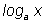   вычисляется сведением к натуральному по формуле замены основания логарифма   log(x)/log(a) синус, косинус, тангенс, котангенс   sin, cos, tan, cot арксинус, арккосинус, арктангенс, арккотангенс   asin, acos, atan, acot Рассмотрим действие указанных в нижнем меню команд на упрощение формул на примере преобразования следующего выражения 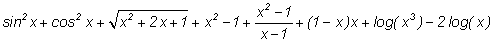1)  Для того чтобы не повторять набор выражения многократно, его можно обозначить функцией от  x, выбрав для функции удобное название. Назовём её  A(x). 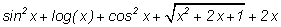Команда определения функции выглядит на этом примере так: A(x):=sin(x)^2+cos(x)^2+sqrt(x^2+2*x+1)+x^2-1+(x^2-1)/(x-1)+(1-x)*x+log(x^3)-2*log(x); 2) Действие команды УПРОСТИТЬ даёт следующий результат: Для получения результата сначала надо ввести выражение, что можно сделать просто набрав имя функции  A(x)  и нажав кнопку ввода, затем останется нажать кнопку с названием команды УПРОСТИТЬ; этого же результата можно добиться прямым вводом команды:  ratsimp(A(x)).  Аналогично выполняются и другие команды. Заметим, что команда упрощения не сделала тригонометрических упрощений и не "избавила выражение от иррациональности". 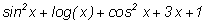3) Действие команды УПРОСТИТЬ (РАЦ) даёт более подходящий результат В этом случае, как мы видим, произошло упрощения выражения с радикалами. Однако тригонометрических преобразований сделано не было. Название команды radcan.  4) Наиболее хороший результат даёт команда УПРОСТИТЬ (ТРИГ): Название команды radcan.  Получить другие примеры работы некоторых команд можно набором команды ПРИМЕР: example. Её аргументом  является команда, примеры применения которой надо получить. Например, для получения примеров по команде УПРОСТИТЬ следует ввести команду example(ratsimp),  результат выполнения которой показан на следующем рисунке.

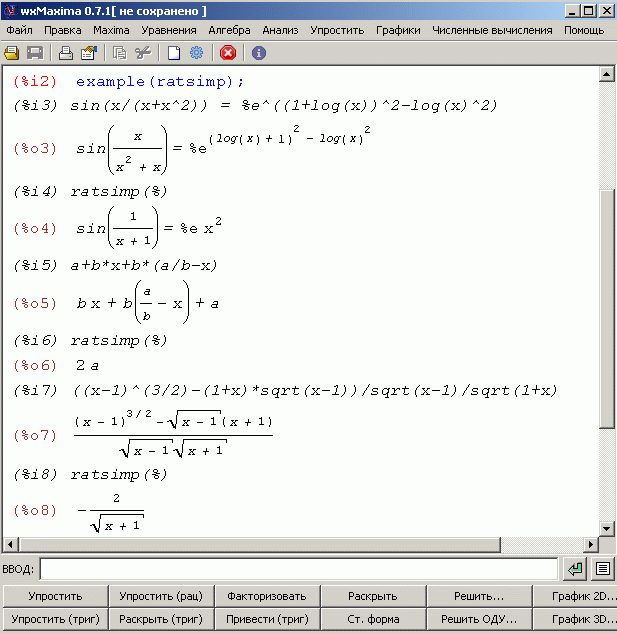Исследовательские работы призваны вывести ученика за рамки школьной комнаты, привлечь его к интеллектуальному богатству различных информационных источников, возбудить интерес к исследовательской деятельности. Преподаватель не должен делать эти работы обязательными, но всячески привлекать ребят к постановкам задач в этих работах и поощрять успехи. Возможно, что одну тему ученик будет разрабатывать в течение полугодия, может быть, это будет группа ребят. Завершиться такое исследование может на школьной или городской конференции.