Показательная функция

Изображение на весь экран - нажать клавишу F11

Показательной функцией называется функция вида y= a^x, где а – фиксированное положительное число,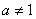

Динамический рисунок графика показательной функции

Свойства показательной функции

Область определения: множество всех вещественных чисел R.
Монотонность: при а > 1 функция у = а^х строго возрастает,
при 0 < а < 1 функция у = а^х строго убывает.
Положительность: значения функции у = а^х положительны (при любом основании а > 0 ).
Область значений: множество всех положительных чисел, т. е. промежуток (0; + ).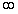

Упражнение. Проиллюстрируйте на динамическом рисунке свойства показательной функции.

Вместе с функцией у = а^х показательной функцией считают и функцию вида у = с а^х, где с – постоянная.

Пример. Функция у = 2 ^{х + 2} = 4

2^х – тоже показательная функция.

Показательные функции обладают еще одним замечательным свойством: скорость их роста пропорциональна значению самой функции.

Прикладные примеры.
1.	Радиоактивный распад. Изменение массы радиоактивного вещества происходит по формуле m = ,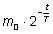
	где	m ₀ – масса вещества в начальный момент t = 0, m – масса вещества в момент времени t, T – период полураспада.


	Закон радиоактивного распада часто записывают в стандартном виде .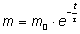
	Связь константы с периодом полураспада: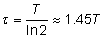
2.	Рост народонаселения. Изменение количества людей в стране на небольшом отрезке времени с хорошей точностью описывается формулой N = N _o e^at,
	где N_o – число людей при t = 0, N – число людей в момент времени t, a – некоторая константа.