| Периодические функции описывают периодически
повторяющиеся процессы. |
|
Пример.
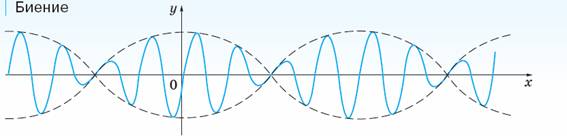
|
| Функция называется периодической,
если существует такое число
T, что
для всех значений аргумента
x
выполняется равенство
f(x+T) =
f(x). Число
T
называется периодом функции. |
Легко видеть, что если
T – период,
то
2T,
3T …
тоже являются периодами.
Сумма, разность, произведение и частное периодических функций с
периодом T
также будет периодической функцией с периодом
T.
Графики периодических функций состоят из периодически повторяющихся
кусков.
|
|
Пример.
Гармонические колебания – это периодический процесс, который может
быть описан периодической функцией вида 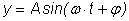 . .
Гармоническое колебание
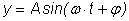 определяется тремя параметрами: амплитудой
A > 0, угловой скоростью
определяется тремя параметрами: амплитудой
A > 0, угловой скоростью
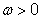 и так называемой начальной фазой и так называемой начальной фазой
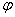 .
Часто вместо угловой скорости .
Часто вместо угловой скорости
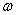 говорят о частоте колебаний говорят о частоте колебаний
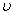 ,
которая связана с угловой скоростью ,
которая связана с угловой скоростью
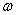 (или иначе круговой частотой) формулой
(или иначе круговой частотой) формулой
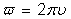 .
Функция y периодична. Ее основной период равен .
Функция y периодична. Ее основной период равен
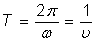 . .
Колебания приходится
складывать. Имеет место замечательный закон: при сложении
гармонических колебаний одной и той же частоты получается снова
гармоническое колебание той же частоты, т.е. сумма двух функций
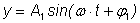 и
и
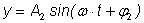 есть функция того же вида
есть функция того же вида
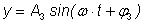 . .
Для сложения функций
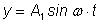 и и
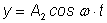 используется прием введения вспомогательного
угла
используется прием введения вспомогательного
угла
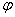 с помощью соотношений с помощью соотношений
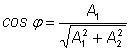 , ,
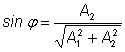 : :
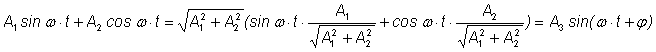
где
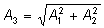 |
| Сумма двух функций с различными периодами не
обязательно будет периодической. |
|
|