| 1. Понятие о статистической обработке числовых
данных При работе с конечными множествами – переборе вариантов,
измерениях, вычислениях, табличном задании зависимостей – появляются
наборы чисел, числовых данных. Для их наглядного представления
используются различные способы: числовой ряд, таблица, график,
диаграмма. |
| 1) Ряд чисел обычно
записывается в виде числовой строки или располагается в
форме столбца. Порядок, в котором идут числа,
обычно определяется тем, в какой последовательности эти числа
появлялись. 2) Простейший способ упорядочить ряд чисел – это
записать их в виде таблицы с двумя входами – в одной строке
таблицы поместить номера или другие понятные обозначения порядка, а
в другой – соответствующие числа. |
Пример.
В классе из 36
человек был проведен опрос, сколько
времени каждый ученик провел вчера у телевизора. Данные этого
опроса приведены в таблице, в которой N
обозначает номер ученика по списку,
t – время в минутах.
|
N |
t |
N |
t |
N |
t |
N |
t |
N |
t |
N |
t |
|
1 |
60 |
7 |
30 |
13 |
15 |
19 |
110 |
25 |
80 |
31 |
70 |
|
2 |
120 |
8 |
100 |
14 |
150 |
20 |
20 |
26 |
50 |
32 |
90 |
|
3 |
90 |
9 |
40 |
15 |
90 |
21 |
60 |
27 |
60 |
33 |
0 |
|
4 |
0 |
10 |
130 |
16 |
0 |
22 |
50 |
28 |
120 |
34 |
30 |
|
5 |
20 |
11 |
0 |
17 |
80 |
23 |
60 |
29 |
90 |
35 |
100 |
|
6 |
90 |
12 |
60 |
18 |
90 |
24 |
100 |
30 |
40 |
36 |
30 |
|
| 3) Координатный метод предлагает
табличные данные изобразить на плоскости. Изобразив в виде точек
одной оси данные, с помощью которых упорядочиваются числа, вторую
координату откладывают в направлении второй оси. Так построенные
точки можно соединить отрезками прямой и получить график в виде
ломаной (его часто называют диаграммой). Если точек
достаточно много, можно соединить их плавной кривой.
4) Графики частот появления результатов.
Очень наглядным приемом является использование той же координатной
системы, но вместо точки на плоскости рисуется прямоугольный
столбик. Такие графики часто называют гистограммами. |
Пример. Как можно
обработать полученные экспериментальные данные
предыдущего примера?
1) Время колеблется от 0 до 150 минут. Разобьем интервал [0; 150] на
десять промежутков времени по 15 минут каждый и подсчитаем, сколько
учеников попадает в каждый промежуток.
В нижней строке таблицы помещены частоты соответствующих значений,
т. е. дроби (а можно было указать проценты), показывающие, какую
часть занимают значения, попавшие в данный интервал, среди всех
значений.
|
[0,15] |
(15,30] |
(30,45] |
(45,60] |
(60,75] |
(75,90] |
(90,105] |
(105,120] |
(120,135] |
(135,150] |
|
5 |
5 |
2 |
7 |
1 |
8 |
3 |
3 |
1 |
1 |
|
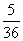
|
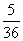 |
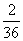 |
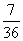 |
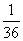 |
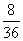 |
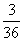 |
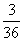 |
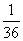 |
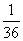 |
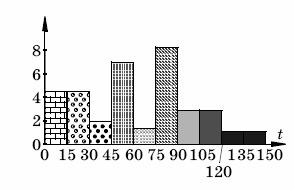
2) Гистограмма распределения числа учеников в
зависимости от проведенного у телевизора времени.
|
5)
Кумулятивные графики частот появления результатов.
Так называют графики, в которых изображается число результатов, не
превосходящих (или не меньших) данного числа. При этом часто число
результатов приводят в процентах.
Для сравнения долей, которые в чем-то целом занимают отдельные
данные, часто используют круговые диаграммы, разделенные на секторы,
отражающие (обычно в процентах) величину этих данных. |
| |
2. Числовые характеристики статистических данных
Все указанные (а также многие другие) способы представления числовых
данных помогают составить о них зрительно, качественное
представление. Более точные, количественные оценки ряда данных
делаются вычислением определенных числовых характеристик этого ряда.
Самой простой и самой распространенной такой характеристикой
является среднее арифметическое, или просто среднее. Если у нас есть
ряд из n
числовых данных
а1, a2, …, an,
то его среднее арифметическое
А
вычисляется по формуле
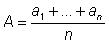 .
.
Помимо среднего арифметического используются иные средние
значения, вычисляемые по другим формулам:
среднее квадратичное
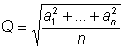 ; ;
среднее гармоническое 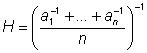 ; ;
среднее геометрическое
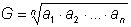 . .
К средним можно отнести также медиану ряда. Она
вычисляется так: числа ряда располагаются в порядке возрастания (они
вначале могли быть расположены по-другому) и берется то, которое по
счету окажется в середине. Такое число находится однозначно, если
количество членов ряда нечетно. В случае, когда их количество четно,
в качестве медианы берут среднее арифметическое двух значений,
оказавшихся в середине.
Бессмысленно ставить вопрос, какое среднее «лучше», точнее
описывает ситуацию. Эту оценку надо делать по смыслу задачи и
учитывать имеющиеся традиции.
Кроме средних значений, используют и другие числовые
характеристики числовых рядов. Например, часто надо учесть не только
среднее значение величины, но и разброс числовых данных вокруг этого
среднего. |
| |