|
Отношение делимости.
Делимость чисел – это отношение, связь между целыми числами. |
Целое число
а делится
на целое число
b, если
существует целое число
q, такое
что
а = bq .
При
этом число
b считается
отличным от нуля.
Число
а называется
делимым,
b называется
делителем, а число
q называется частным. |
| Также говорят: "a
кратно b". Числа
1 и
–1 являются делителями любого целого числа. Число
0 делится на любое число, в том числе и на ноль, но ни
одно целое число, отличное от нуля, не делится на
0. |
|
Например,
положительными делителями числа
132 являются числа
1, 2, 3, 4, 6, 11,12, 22, 33, 44, 66, 132. Эти же числа,
взятые со знаком
«–» также будут делителями числа
132. |
Если
d – делитель числа
n, то и число
- d также является его делителем. При изучении делимости
можно ограничиться только натуральными числами.
Вместо слов «n делится на
d» можно сказать «d
делит
n». Для такого высказывания применяется стандартное
обозначение
d | n. Однако оно не очень удобно, потому что привычнее
говорить «n делится на
d», что часто обозначают как
 . |
|
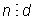Отношение делимости обладает следующими свойствами.
1) Если два числа делятся на
d, то и их сумма делится на
d.
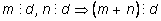
2) Если число
n делится на
d, то и число
nk при любом
k делится на
d.
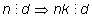
3) Если
m делится на
n, а
n делится на
d, то
m делится на
d.
 |
|
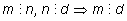Доказать свойства делимости довольно легко. Возьмем для
примера первое свойство.
Условия
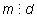и
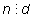означают, что существуют числа
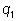и
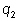такие, что
,
 .
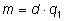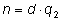Сложим эти два равенства:
 .
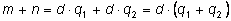Равенство
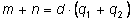означает по определению делимости, что
m + n делится на
d.
Два других свойства доказываются аналогично.
На
основе свойств делимости выводятся признаки делимости.
|
|
Пример. Признак делимости на
4: "Задано натуральное число в десятичной записи. Если
число, образованное его последними двумя цифрами,
делится на
4, то и исходное число делится на
4 ".
Например, для шестизначного числа:
a5
105
+ a4
104
+
... + a1
10 +
a0 = 100 (a5
1000
+ a4
100
+ a3
10
+ a2 )+ a1
10 +
a0.
Первое из чисел делится на
4, так как
100 делится на
4.
Значит всё число делится на
4 тогда и только тогда, когда
10a1
+
a0 делится на
4. |
Упражнения. Используя инструмент
проверьте следующие признаки делимости:
1. Признак делимости на 4.
2. Признак делимости на 3.
3. Нажимая многократно кнопку генерации
шестизначных чисел - "проверить новое шестизначное число" - найдите
число, делящееся на 11. Подберите коэффициенты линейной комбинации
цифр, при которой она тоже делится на 11. Проверьте
предполагаемый признак на других шестизначных числах, продолжая
нажимать кнопку генерации. |
|
|
Простые и составные числа.
Отношение делимости позволяет раскладывать целые числа на
множители. |
| Простое число – это
натуральное число
n > 1 , не имеющее других положительных делителей,
кроме самого себя и единицы. |
|
Числа
2,
3,
5,
7,
11 являются первыми простыми числами.
Приведем перечень простых чисел, меньших
100: 2,
3,
5,
7,
11,
13,
17,
19,
23,
29,
31,
37,
41,
43,
47,
53,
59,
61,
67, 71,
73,
79,
83,
89,
97.
Простые числа образуют основные кирпичики при изучении делимости целых
чисел и решении связанных с этим понятием задач.
Простые числа образуют основные кирпичики при изучении делимости целых
чисел и решении связанных с этим понятием задач.
Все числа, которые не являются простыми, называются составными.
Если взять два составных натуральных числа
m и
n , то у них есть делители, отличные от этих чисел и не
равные единице. |
| Два числа называются взаимно
простыми, если они не имеют общих делителей, кроме
1. |
Например, числа
25 и
32 взаимно простые (хотя ни одно из них простым
не является).
Взаимно простыми могут быть и несколько чисел, например, числа
6, 10, 15 взаимно простые (хотя никакие два из
них взаимно простыми не являются).
Наибольший общий делитель и наименьшее общее кратное.
Возьмем два натуральных числа
m и
n . Среди всех общих делителей этих чисел выберем
наибольшее и обозначим через
d. Часто наибольший общий делитель обозначают
буквами НОД:
d = НОД (m, n). Заметим, что число
1 является общим делителем, поэтому множество общих
делителей является непустым конечным множеством чисел и в нем можно
выбрать наибольшее число.
Если
НОД (m, n) = 1, то числа
m и
n будут взаимно простыми.
Похожим образом определяется наименьшее общее кратное двух
или нескольких чисел. Число
mn делится и на
m, и на
n, т. е. является общим кратным
m и
n . Наименьшее из общих кратных часто обозначают буквами НОК.
Например,
НОД (240, 36) = 12;
НОК (240, 360) = 720. |
| |