Деление с остатком.
Пусть даны два целых числа
m и
n (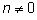 ). ).
Мы говорим, что делим m на n с остатком, когда
представляем m в виде
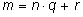 ,
где
q и
r целые числа, причём
r удовлетворяет неравенствам ,
где
q и
r целые числа, причём
r удовлетворяет неравенствам
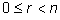 . .
Число
q называется частным, а
r остатком от деления
m на
n.
Если r = 0, то получается
определение делимости
m на
n. |
Примеры.
1)
35 = 8*4+3, то есть частное от деления
36
на
8 равно
4, а остаток равен
3;
2)
-35=8*(-5)+5, остаток равен
5;
3) тот же остаток получится при делении
(-35) на
(-8):
-35=(-8)*5+5, остаток равен
5, а не
(-3), как можно было предположить
по аналогии с делением
35 на
8 (!) |
| |
|
|
|
|
Упражнения. Используя инструмент
представления пары чисел в форме деления с остатком, выполните
следующие упражнения:
1. Проиллюстрируйте на предложенном
инструменте приведённые выше примеры.
2. Найдите такую пару чисел, чтобы остаток от деления
большего на меньшее был равен частному.
Может ли остаток быть равен делителю?
3. Найдите такую пару чисел, чтобы остаток от деления
большего по абсолютной величине на меньшее был противоположен
частному (то есть получался умножением на -1). Какое из
этих чисел будет отрицательным? Почему?
4. Как изменятся остаток от деления от одного числа на
другое, если изменить знак делителя на противоположный. Сначала
сформулируйте гипотезу, потом проверьте с помощью инструмента. |
| |
Теорема. Деление с остатком
определено для любой пары целых чисел
m и
n (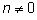 ),
причём частное и остаток определяются единственным образом. ),
причём частное и остаток определяются единственным образом. |
Доказательство.
1) Докажем существование. Положим для определённости
m > n. Рассмотрим
числа
n, 2n, 3n, 4n, …..qn, (q+1)n, …. Число
m будет находиться между
какими-то соседними из этих чисел, пусть это будут
qn и (q+1)n (это
достаточно очевидно и относится к аксиоматике чисел, то есть
принимается без доказательства): 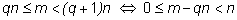
Обозначив
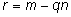 ,
получим доказательство существования. ,
получим доказательство существования.
2) Единственность докажем от противного.
Пусть имеется два разложения:
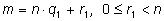 и
и
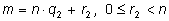 . .
Вычитая одно из другого, получим:
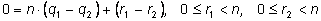 , ,
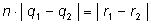
Если
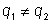 , то
выражение слева не меньше
1, так как , то
выражение слева не меньше
1, так как
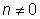 .
В то же время, выражение справа меньше
1, так как это величина разности двух чисел,
меньших
1. Получаем противоречие, откуда следует, что .
В то же время, выражение справа меньше
1, так как это величина разности двух чисел,
меньших
1. Получаем противоречие, откуда следует, что
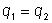 ,
а значит и ,
а значит и
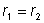 ,
что и означает единственность представления. ,
что и означает единственность представления. |
Алгоритм Евклида
|
|
Алгоритм Евклида даёт эффективный способ нахождения НОД двух чисел.
Алгоритм Евклида основан на делении с остатком.
Взяв два натуральных числа
m
и
n
(делимое и делитель),
мы будем заменять большее
из них остатком до тех пор, пока не получится нулевой остаток.
Последний ненулевой остаток и будет наибольшим общим делителем чисел
m
и
n. |
|
|
Пример применения
алгоритма Евклида.
|
Первое число |
Второе число |
Деление нацело |
Остаток |
|
3367 |
1001 |
3367 = 1001×3 + 364 |
364 |
|
364 |
1001 |
1001 =364 ×2 + 273 |
273 |
|
364 |
273 |
364 = 273 ×1 + 91 |
91 |
|
91 |
273 |
273 = 91×3 + 0 |
0 |
|
91 |
0 |
|
|
Получили, что
НОД (3367, 1001) = 91. |
|
|
|
Упражнения.
1. Проделайте операции по вычислению наибольшего общего
делителя (НОД) с помощью представленных выше встроенных
инструментов.
2. Возьмите наугад два числа: четырёхзначное и трёхзначное.
Найдите их НОД с помощью инструмента.
(Если не хватит полей, можно досчитать устно или продолжить,
переходя к первому инструменту). |
|
|
| Теорема. Алгоритм Евклида
приводит к нахождению наибольшего общего делителя любой пары
натуральных чисел. |
Доказательство.
Пусть числа
m и n
(m > n) имеют общий делитель
d. Представим число
m в виде
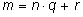
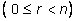 ,
откуда
r = m - nq, следовательно,
r делится на
d. Таким образом, получившиеся после замены
большего числа остатком числа
n и
r имеют те же делители, что и числа
m и
n. ,
откуда
r = m - nq, следовательно,
r делится на
d. Таким образом, получившиеся после замены
большего числа остатком числа
n и
r имеют те же делители, что и числа
m и
n.
Этот процесс обязательно закончится, так как остатки все время уменьшаются
и в то же время остаются неотрицательными. Следовательно, на каком-то
шаге остаток окажется равным нулю.
Пусть
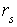 – последний ненулевой остаток, тогда числа
– последний ненулевой остаток, тогда числа
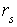 и
0 имеют те же делители, что и числа
m и
n.
и
0 имеют те же делители, что и числа
m и
n.
Это и означает, что последний остаток является НОД чисел
m и
n.
Расширенный алгоритм Евклида.
Проследите за вычислениями в последнем столбике таблицы (снизу вверх).
|
Первое число |
Второе число |
Деление нацело |
Обратный ход алгоритма Евклида |
|
3367 |
1001 |
3367 = 1001×3 + 364 |
91 = (3367 – 1001×3 ) ×3– 1001×1 =
=
3367 ×3 +
1001×(–10 ) |
|
364 |
1001 |
1001 =364 ×2 + 273 |
91 =
364 – (1001 –
364 ×2) =
= 364 ×3– 1001×1 |
|
364 |
273 |
364 = 273 ×1 + 91 |
91=364 – 273 ×1 |
|
91 |
273 |
273 = 91×3 + 0 |
0 |
На последнем шаге (в верхней строчке) получаем выражение, которое
называется линейным представлением НОД:
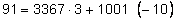 |
Определение. Линейным
представлением наибольшего общего делителя
d чисел
m и
n называется представление
d в виде:
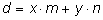 ,
где
x и
y некоторые целые числа. ,
где
x и
y некоторые целые числа. |
| Из примера ясно, как строится линейное представление
НОД. |