| Важнейшим достижением греческой античной математики
является доказательство двух основных теорем, приписываемых Евклиду
(IV век до н. э.). |
| Теорема. Всякое
натуральное число можно разложить на простые множители, т. е.
однозначно записать его в виде произведения степеней простых чисел. |
|
Например, число
12600 имеет такое разложение на простые множители:
 . |
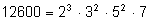| Теорема. Ряд простых
чисел бесконечен. |
Например, сотым по счету простым числом будет число
р = 523. Однако как бы ни было велико простое
число
р, всегда найдется большее его другое простое
число. |
|
Чебышёв |
|
Пафнутий Львович |
|
|
Годы жизни: |
|
1821-1894 |
Распределение
простых чисел в натуральном ряду очень неравномерно и всегда
привлекало внимание математиков своими загадками. Ряд глубоких
результатов о простых числах был получен в XIX-XX веке. Например,
замечательный русский математик П. Л. Чебышев в 1850 году доказал так
называемый асимптотический закон распределения простых чисел,
указывающий примерную долю простых чисел среди всех натуральных чисел.
С другой стороны, ряд гипотез о простых числах остается недоказанным.
Например, легко заметить, что простые числа иногда встречаются парами,
«близнецами»:
17 и
19,
41 и
43,
311 и
313 и т. п. До сих пор не доказано, существует ли
бесконечное количество близнецов или нет. |
| Основная теорема арифметики.
Всякое число, большее
1, может быть разложено в произведение простых
чисел, и это разложение единственно с точностью до порядка множителей. |
Доказательство.
Пусть
a – целое число, большее единицы. Обозначим через
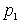его наименьший простой делитель, тогда
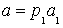. Если
 ,
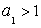то обозначим через
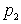его наименьший простой делитель, т.е.
 .
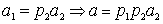Если
 ,
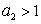то также представим
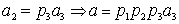и т.д. В конце концов, мы получим
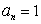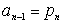и
и
 .
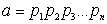Если предположить, что число
a раскладывается на простые множители другим
способом:
 ,
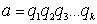то получим, что
 .
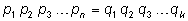Справа число делится на
 ,
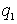следовательно, и число слева делится на
,
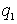а тогда среди множителей есть по крайней мере один, который делится на
,
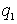но так как все множители простые, то этот множитель (будем считать,
что это
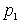) равен
.
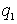Сократим обе части равенства на
,
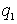получим
=
 .
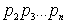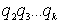Теперь повторим рассуждения с множителем
 ,
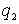получим
=
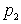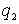и т.д. |
Замечание. В разложении числа на простые сомножители многие из них
могут повторяться, поэтому в общем виде разложение числа
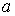на простые множители с учетом их кратности можно
записать так:
 ,
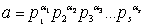где
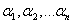– целые числа и их сумма равна
n. |
Использование разложения на множители для нахождения наибольшего
общего делителя и наименьшего общего кратного.
Если числа не очень велики, то их легко разложить на множители и затем
выписать общие множители и их перемножить. Например,
НОД (24, 36) = НОД ( )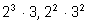
=
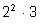= 12;
НОК (24, 36) = НОК ()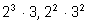
=
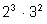= 72.
По этому примеру видно правило нахождения НОД и НОК, если данные числа
разложены на простые множители.
Если же числа очень большие, то потребуются первые сотни или тысячи
простых чисел, которые довольно трудно определить. Таким образом, этот
(известный из учебников основной школы) метод является на самом деле
неэффективным и на практике не применяется.
Например, в процессе разложения на множители Вы получили число
528705743. Можно ли продолжить разложение на
множители или получилось простое число? |
| Теорема (о бесконечности
множества простых чисел). Ряд простых чисел бесконечен. |
Доказательство.
Предположим, что простых чисел конечное число. Перечислим их:
 .
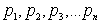Составим число
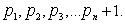Это число не делится ни на одно из чисел
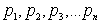(даёт остаток
1 при делении на каждое из этих чисел), а следовательно,
оно делится только на
1 и на себя. Мы получили новое простое число, которого
нет среди чисел
.
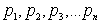Продолжая этот процесс, мы будем получать все время новые простые
числа, т. е. их не может быть конечное число. |
| |