Изображение на весь экран - нажать клавишу F11

СРАВНЕНИЯ

Классы вычетов.
Если данное число m записано в десятичной системе счисления, то разделить его с остатком на 10 очень легко – остатком будет последняя цифра, а неполным частным – число, получающееся зачеркиванием последней цифры:
.
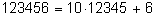Вам, возможно, знакомо такое простое правило – если мы хотим найти последнюю цифру некоторого числового выражения, надо выполнить все операции с последними цифрами этих чисел, т. е. заменить все числа их остатками при делении на 10. Это правило обобщается для нахождения остатка при делении на любое число n. Для этого введем понятие сравнения.

Число a называется сравнимым с числом b по модулю m, если разность a – b делится на m. Для сравнений по модулю m употребляется следующая запись: .

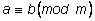Можно дать другое определение сравнимости:

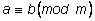, если a и b имеют одинаковые остатки при делении на m.

Примеры.
1) ,
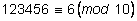2) ,
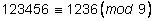3) .

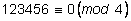Упражнения. С помощью инструмента представления целого числа в виде деления с остатком на целое ненулевое выполните следующие упражнения.
1. Проверьте примеры, приведённые выше.
2. Какова закономерность остатков от деления последовательных степеней двойки на 7?
3. Используя дополнительно встроенный калькулятора, найдите закономерность от деления седьмых степеней натуральных чисел на семь (проверьте устно для 1, далее для 2, 3, 4, 5, 6, 7, 8, 9, 10).

Зафиксируем модуль m > 1. Все числа, сравнимые между собой по модулю m, можно объединить вместе. Такое множество называется классом вычетов по модулю m. Все числа в одном классе вычетов имеют один и тот же остаток при делении на m, а числа в разных классах имеют разные остатки. Выпишем для примера классы вычетов по модулю 5.
0, 5, 10, 15, 20, 25, 30, …
1, 6, 11, 16, 21, 26, 31, …
2, 7, 12, 17, 22, 27, 32, …
3, 8, 13, 18, 23, 28, 33, …
4, 9, 14, 19, 24, 29, 34, …
Классы вычетов по модулю m представляют собой арифметические прогрессии с разностью m. Классы удобно дополнить отрицательными целыми числами. Например, в класс чисел по модулю 5, сравнимых с числом 4, попадут такие числа: …, –11, –6, –1, 4, 9, 14, …

Свойства сравнений.
Главный принцип операций со сравнениями состоит в том, что если нас интересует только остаток от деления числового выражения на число m, в числовом выражении мы можем заменять числа в этом выражении на любые другие, сравнимые с ними по модулю m, т. е. любые другие из того же класса вычетов.

Примеры применения сравнений для решения задач на делимость.
1) Доказать, что число 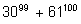делится на 31.
Рассмотрим сравнение по модулю 31:

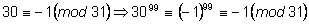
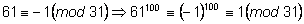
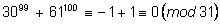, что и требовалось доказать.
2) У числа 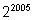находят сумму его цифр. Затем у получившегося числа снова находят сумму его цифр, и этот процесс повторяют до тех пор, пока не получится однозначное число. Найти это число.
По признаку делимости на 9 число a и сумма его цифр имеют одинаковые остатки при делении на 9, т. е. они сравнимы между собой по модулю 9. Найдем этот остаток для числа .
,
,
,
,
,
,
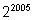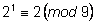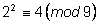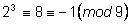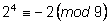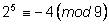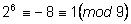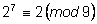и т. д.
Видно, что так как 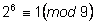, то остатки по модулю 9 у степеней двойки будут повторяться периодически с периодом 6, т.е. 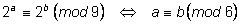. Так как 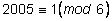, то 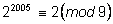, т. е. ответом будет число 2.

Выполненные примеры основаны на следующих свойствах сравнений.
Свойства сравнений.
1) Сравнения можно складывать:

.
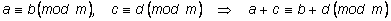2) Сравнения можно перемножать:

.
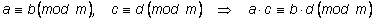Доказательство.
Докажем второе из этих свойств. Запишем определения:

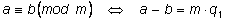
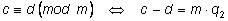
Перемножим равенства

.
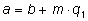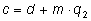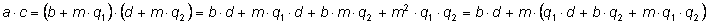Из последнего равенства следует, что 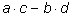делится на m, т. е.

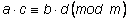, что и требовалось доказать.

Рассмотрим вопрос о делении сравнений. Пусть дано сравнение 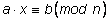. Можно ли обе его части поделить на а, чтобы найти x? Оказывается, что это всегда можно, когда коэффициент a является числом, взаимно простым с модулем n. Условие взаимной простоты в сравнениях заменяет условие 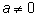для решения уравнений .

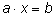Теорема. Если число a взаимно просто с числом m, то у него есть обратное по модулю m, т. е. существует такое целое число x, что

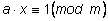Доказательство.
Применим теорему о линейном представлении НОД для взаимно простых чисел a и m, для которых d = НОД (a, m) = 1: 1 = x * a + y* m. Из этого равенства следует, что

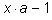делится на m, т. е.

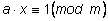, что и требовалось доказать.

Арифметика остатков.
При выполнении арифметических действий часто в качестве представителей классов вычетов по модулю m берут остатки от их деления на
m: 1, 2, 3,…, m–1. В этом случае вместо отношения сравнимости можно использовать знак равенства и говорить, что арифметические операции выполняются в арифметике сравнений по модулю m на множестве {1, 2, 3,…, m–1}.

Пример. Построим таблицы сложения и умножения для классов вычетов по модулю 5.

+	0	1	2	3	4		1	2	3	4
0	0	1	2	3	4	0	0	0	0	0
1	1	2	3	4	0	1	1	2	3	4
2	2	3	4	0	1	2	2	4	1	3
3	3	4	0	1	2	3	3	1	4	2
4	4	0	1	2	3	4	4	3	2	1

По этим таблицам легко делать вычисления в арифметике остатков по модулю 5. Например, 3+4=2, 4*4=1. Нетрудно догадаться, как с помощью таблиц выполнить и обратные операции: 1–3=3, 3/4=2.

Замечание. Когда числа маленькие, для деления остатков (и для нахождения обратного) можно применить простой приём: добавлять к числителю величину модуля m, пока числитель не поделится нацело. Частное и будет искомым остатком.

Пример.

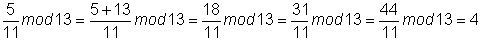
<< назад вперед >>

В оглавление модулей / В расписание уроков