|
Числовой фокусник просит: «Умножьте номер дня
вашего рождения на
12, номер месяца на
31, сложите эти числа и скажите мне сумму». Я
вычисляю и называю число
182. Фокусник немедленно объявляет, что я родился
10 февраля. |
|
Как
он рассуждал?
Если обозначить номер дня рождения через
x, а номер месяца через
y, то мой ответ дает одно соотношение между
x и
y:
12x + 31y = 182. Ясно, что есть бесконечно
много чисел
x и
y, удовлетворяющих этому уравнению. Как же
фокусник нашел дату моего рождения?
Приведенная
задача является типичной задачей на нахождение целочисленных решений
уравнения.
Такие задачи возникают очень часто. Их называют диофантовыми по имени
древнегреческого математика Диофанта (III век), в книге которого «Арифметика»
до нас дошло более ста задач на нахождение целых решений. |
|
Найдем все
целочисленные решения (не обязательно положительные) решения уравнения
12x + 31y = 182.
Рассмотрим это уравнение по модулю
12.
Получим
 .
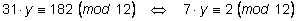Так как
НОД (7, 12) = 1,
то можно найти класс вычетов, обратный к классу
7
по модулю
12,
т. е. попросту подобрать число
a
так, чтобы
7а
было бы сравнимо с
1
по модулю
12.
Подбор осуществляется легко:
a
можно взять равным
7
(или
–5,
что облегчает выкладки).
Умножим сравнение
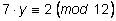на
(–5):
 .
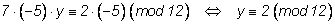Итак, любое число
y
вида
2 + 12t,
где
t
– целое
число, удовлетворяет сравнению
 .
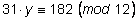Подставим
y
в исходное
уравнение :
 .
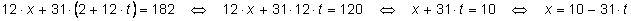Итак, пара чисел
(10 – 31t; 2 + 12t)
при любом целом
t
является целочисленным
решением данного уравнения.
Легко проследить рассуждение и убедиться,
что мы нашли все целочисленные решения.
В прогрессиях
x = 10 – 31t; y = 2 + 12t лежит
бесконечно много целочисленных решений.
По условию
 .
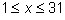В этих границах нет двух значений
x,
принадлежащих прогрессии со знаменателем
31.
Аналогичное верно и для
y.
Поэтому есть только одна пара чисел
(x; y),
у которой
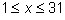и одновременно
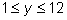– это пара
(10; 2),
которая и соответствует дате
10
февраля, найденной фокусником. |
|
Теория
диофантовых уравнений является одним из самых интересных и трудных
разделов математики. Многие гипотезы этой теории остаются
недоказанными и по сей день, несмотря на усилия лучших математиков.
Самое крупное достижение математики последних лет – доказательство
Великой теоремы Ферма, полученное английским молодым ученым А. Уайлсом,
– относится к теории диофантовых уравнений. |
|
Теорема Ферма.
Уравнение
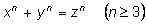не имеет
целочисленных решений, кроме очевидных, когда одно из неизвестных
равно нулю. |
|
Аналогичное уравнение
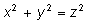для
n = 2 имеет
бесконечно много целочисленных решений. Они образуют «пифагоровы
тройки» – наборы натуральных чисел, которые могут быть сторонами
прямоугольного треугольника:
(3, 4, 5), (5, 12, 13), (8, 15, 17)
и др. Решение этого уравнения было известно в древней Индии,
переоткрыто древнегреческими математиками и доступно любому школьнику.
|
|
Формулы
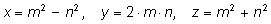 являются старинными формулами для «пифагоровых троек». |
| |
