Изображение на весь экран - нажать клавишу F11
 
НЕПРЕРЫВНЫЕ ДРОБИ
 
Определение.  Пусть 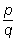   рациональное число, где  q > 0.

Представлением рационального числа в виде непрерывной (часто её называют ещё цепной) дроби называется его представление в виде:

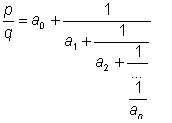
где все числа 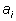   целые, причём отрицательным может быть только  .
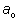Для удобства непрерывную дробь записывают в виде 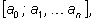   где целая часть отделяется от остальной части точкой с запятой, а остальные члены – запятой.
Теорема.  Любое рациональное число 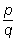   имеет представление в виде конечной непрерывной дроби, причём оно единственно, если считать  
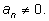Доказательство.
По теореме о делении с остатком имеется единственное представление 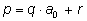 ,  где все числа целые, а 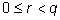 .  Разделив на  q,  получим единственное представление  ,  где 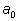  - целое, а 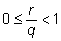 .  Если 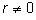 ,  процесс можно продолжить:
                 

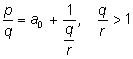
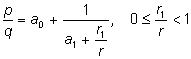
Заметим, что последовательность остатков убывает: 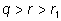 .  Так как это целые неотрицательные числа, то через конечное число шагов остаток станет равным нулю и процесс остановится. Получим непрерывную дробь, которая в силу единственности деления нацело также единственна.
Нетрудно заметить, что алгоритм построения непрерывной дроби есть не что иное, как алгоритм Евклида.

Упражнения.  Прежде чем прочитать следующий пример, выполните упражнения, используя инструмент деления с остатком.
1. Найдите представление в виде непрерывной дроби числа  .
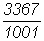2. Найдите представление в виде непрерывной дроби числа 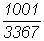 .  Чем эта непрерывная дробь отличается от предыдущей? Объясните ответ.

3. Найдите рациональные числа, представления которых непрерывными дробями состоят из одних единиц.
   = * +
   = * +
   = * +
   = * +
   = * +
 

Пример.

Числитель

Знаменатель

Деление нацело

Построение непрерывной дроби

3367

1001

3367 = 1001×3   + 364

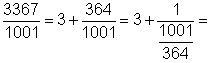364

1001

1001 =364 ×2   + 273

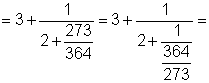364

273

364 = 273 ×1  + 91

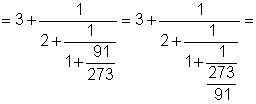91

273

273 = 91×3   + 0

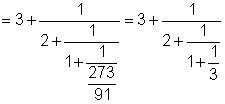Подходящие дроби.
  Если мы будем обрывать процесс вычисления на первом, втором, третьем и т. д. шаге, то получим конечные дроби 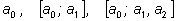    и т.д., которые будем называть подходящими дробями.
Обозначим 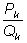   k - ую подходящую дробь 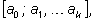   записанную в виде обыкновенной дроби.
Таким образом, две первые подходящие дроби имеют вид: 

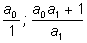
Числа 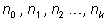   называются неполными частными.

Оказывается, что подходящие дроби в некотором смысле являются наилучшими приближениями рационального числа, представленного непрерывной дробью.
 
 
<< назад               вперед >>
В оглавление модулей / В расписание уроков