|
Системы записи чисел
|
Пифагор |
|
Πυθαγόρας |
 |
|
Годы жизни:
|
|
570
– 490 д.н.э. |
Легендарному
Пифагору приписывают слова: «Все есть число». Один из последователей
Пифагора писал: «Если бы не число и его природа, ничто существующее
нельзя было бы постичь ни само по себе, ни в его отношении к другим
вещам. Мощь чисел проявляется во всех деяниях и помыслах людей, во
всех ремеслах и музыке».
Числам приписывали магические свойства многие древние цивилизации.
В основе понятия натурального числа лежит представление о том, что
значит, что в двух множествах количество предметов одинаково.
Натуральное число выражает общее свойство всех множеств, имеющих
одинаковое количество предметов, элементов.
Математика использует различные символы для обозначения чисел,
создает системы записи.
Наиболее распространенной является
десятичная система счисления. В ней выбраны символы для записи
нуля и первых девяти натуральных чисел – это арабские цифры
0,
1,
2, 3,
4,
5,
6,
7,
8,
9. |
|
Каждое натуральное число n однозначно
можно представить в виде
 ,
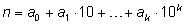где
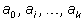 – цифры,
десятичные знаки числа
n,
причем последняя цифра
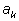отлична от нуля.
Число n записывается
последовательностью цифр
 ,
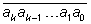начиная со старших разрядов.
|
|
Замечание. В определении используется обратный порядок, так как
обычно, например, при переводе чисел из одной системы счисления в
другую, цифры числа находятся "с конца".
 Используются другие позиционные системы счисления, в которых в
качестве основания выбирается произвольное натуральное число
а ≠
0, фиксируются обозначения для «цифр», т. е. чисел от
1 до
а – 1 (плюс
символ для обозначения нуля). Представление числа n в виде
суммы степеней числа а с коэффициентами
от нуля до a–1
:
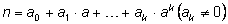позволяет записать число
n последовательностью цифр в системе счисления с основанием а.
Широко распространены двоичная (а = 2) , троичная (а
= 3) , восьмеричная (а
= 8) , двенадцатеричная (а
= 12) системы счисления.
Заметим,
что позиционная система счисления не является единственной
распространенной системой записи натуральных чисел. На рисунке
изображена обложка современной книги, на которой год издания записан
римскими цифрами. Эта запись не является
позиционной. |
|
Упражнения. С помощью следующего
инструмента выполните упражнения.
1. Проверьте правильность указания года издания на книге.
2. Переведите устно текущий год в римскую запись.
Проверьте с помощью инструмента.
3. Напишите правильную на ваш взгляд последовательность римских
цифр некоторого числа. Проверьте корректность с помощью инструмента.
Переведите число в десятичную запись сначала устно, затем с помощью
инструмента. |
|
Преобразователь чисел выполнен в виде Java-скрипта.
Находится в коллекции свободного доступа и может
быть включен в HTML-страницы
простым копированием.
This free script provided by
JavaScript Kit
|
|
Задания*. Используя свои знания по информатике выполните
следующие задания.
1. Сформулируйте алгоритм перевода числа из римской
записи в десятичную. Реализуйте алгоритм на известном вам языке
программирования.
2*. Сформулируйте алгоритм перевода числа из
десятичной записи в римскую. Реализуйте алгоритм на известном вам
языке программирования.
3**. Сформулируйте алгоритм перевода "неправильной"
римской записи в правильную, проведя предварительные эксперименты с
инструментом коррекции числа в римской записи. |
|
|
| Множество всех
натуральных чисел обозначается буквой N. Целые
числа получаются из натуральных добавлением к множеству N
нуля и отрицательных целых чисел – натуральных чисел,
снабженных знаком минус. |
|
В множестве
Z целых чисел определены
арифметические операции (сложение и умножение), обладающие
определенными свойствами (переместительный, сочетательный,
распределительный законы и т. п.)
В множестве Z есть два важных отношения: неравенства и
делимости.
Отношение неравенства (больше – меньше) позволяет
упорядочить все целые числа. Свойства неравенств позволяют следить
за тем, как сохраняется или меняется этот порядок при выполнении
арифметических операций. Натуральные числа считаются положительными
целыми числами. Отношение делимости будет обсуждаться подробно в следующем
разделе. |
| |