|
Теорема Безу.
Теорема Безу, несмотря на внешнюю простоту и очевидность, является
одной из фундаментальных теорем теории многочленов. В этой теореме
алгебраические свойства многочленов (которые позволяют работать с
многочленами как с целыми числами) связываются с их функциональными
свойствами (которые позволяют рассматривать многочлены как функции). |
|
Теорема Безу. Остаток от деления
многочлена
F(x) на линейный двучлен
x–a равен значению многочлена в точке
а, т. е. числу
F(a). |
|
Доказательство.
Разделим
F(x) на
x–a с остатком, т. е. представим его в виде
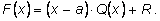Как было сказано выше, остаток
R является константой. Подставим
x=a : 
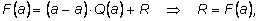что и требовалось доказать.
|
|
Следствие.
Для того чтобы многочлен
F(x) делился на двучлен
x–a, необходимо и достаточно, чтобы
F(a)=0, т. е. чтобы
а было корнем многочлена
x. |
|
Схема Горнера. |
|
Схема Горнера – это алгоритм деления многочленов,
записанный для частного случая, когда частное равно двучлену
x–a. |
|
Построим этот алгоритм.
Пусть
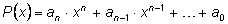– делимое,
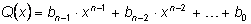- частное (его степень, очевидно, будет на
1 меньше),
r - остаток (так как деление осуществляется
на многочлен
1-ой степени, то степень остатка будет на
1 меньше, то есть нулевая, значит, остаток –
константа).
По определению деления с остатком
P(x) = Q(x) (x–a) + r. После подстановки выражений
многочленов получим:
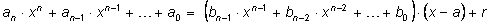
Раскроем скобки и приравняем коэффициенты при одинаковых степенях,
после чего легко выразить коэффициенты частного через коэффициенты
делимого и делителя. |
|
Коэффициенты при одинаковых степенях |
Выражение
коэффициентов bk
через коэффициенты ak |
|
an
= bn-1
|
bn-1
= an
|
|
an-1 = bn-2 – a bn-1
|
bn-2 =
a bn-1
+ an-1
|
|
…
|
…
|
|
ak
=
bk-1
– a bk
|
bk-1
=
ak +
a bk
|
|
…
|
…
|
|
a0
=
r – a b0
|
r
=
a b0
+
a0
|
|
Обычно вычисления сводятся в следующую таблицу.
|
a |
an |
… |
… |
ak |
… |
a0 |
|
|
bn-1
=
an |
…
|
bk |
bk-1
= ak
+
a bk |
… |
r
= a b0
+
a0
|
Здесь выделены те клетки, содержимое которых участвует в
вычислениях на очередном шаге. |
Пример.
Пусть надо поделить многочлен
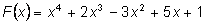на двучлен x–2. Составим
таблицу с двумя строками. В первую строку выпишем коэффициенты данного
многочлена. Во второй строке будут получаться коэффициенты неполного
частного по такой схеме: сначала переписывается старший коэффициент
данного многочлена, затем, чтобы получить очередной коэффициент,
умножают последний найденный на
а=2 и складывают с соответствующим коэффициентом
многочлена
F(x). Самый последний коэффициент будет остатком,
а предыдущие – коэффициентами неполного частного.
|
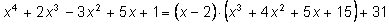
a = 2 |
1 |
2 |
–3 |
5 |
1 |
|
1 |
4 |
5 |
15 |
31 |
1*2+2=4;
4*2+(-3)=5; 5*2+5=15;
15*2+1=31 |
|
|
Упражнения.
1. Проделайте
вычисления по схеме Горнера из предыдущего примера, используя
простой инструмент умножения и сложения (среднее поле меняться не
будет - для предыдущего примера его значение будет равно 2).
2. Вычислите значение многочлена
x7 + 3x6 - 5x4 + 2x3
+ 7x2 - 11x + 17 при
x = 2,
попутно найдя коэффициенты неполного частного. Попробуйте
вычислить это значение без схемы Горнера! |
| |