Число корней многочлена
Пусть
F(x) – многочлен степени
n с вещественными коэффициентами. То, что
вещественных чисел недостаточно для описания корней многочлена, стало
ясно еще после работ итальянцев в XVI веке и привело к расширению
множества вещественных чисел до множества комплексных чисел, которые
будут обсуждаться позже.
Нахождение корней многочлена тесно связано с его разложением на
множители. Если
а – корень многочлена
F(x), то из теоремы Безу следует, что
F(x) делится на
x–a, т. е.
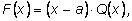где многочлен
Q(x) имеет степень, на единицу меньшую, чем
F(x). Дальнейшие поиски корней многочлена
F(x) сводятся к поиску корней многочлена
Q(x).
Если число
b является другим (отличным от
а ) корнем многочлена
F(x) , то
b является корнем многочлена
Q(x). Действительно, подставляя
x=b, получаем
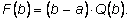Если
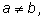то
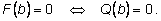С другой стороны, число а тоже может быть корнем многочлена
Q. Тогда
Q(x) делится на
x–a, т. е.
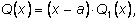и мы получим, что многочлен
F(x) делится на
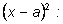
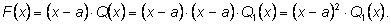В этом случае говорят, что
x=a является кратным корнем многочлена
F. В общем случае кратностью корня
x=a многочлена
F(x) называют наибольшую степень двучлена
(x – a), на которую делится многочлен
F(x): |
k – кратность корня
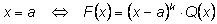и
 |
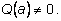Пример.
Многочлен
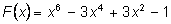так может быть разложен на множители:
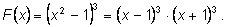Из этого разложения видно, что он имеет два корня
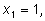
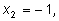причем кратность каждого из них равна
3. |
Упражнения.
1. Используя схему Горнера, с помощью
прилагаемого инструмента проверьте, что
x = 3
является корнем
следующего многочлена
x7 - 6x6
+ 5x5
+ 3x4
+ 115x3
- 360x2
+ 351x -
189.2. Используя частное полученное при
делении многочлена по схеме Горнера, определите корнем какой
кратности является
x = 3.
|
|
|
|
Теорема. Число вещественных корней
многочлена а
F не может быть больше его степени. |
Следствия
1) Если число различных корней многочлена больше его степени, то
многочлен – нулевой, т. е. все его коэффициенты равны нулю.
2) Теорема о тождестве. Если два многочлена
F(x) и
G(x), степень которых меньше или равна
n, принимают одинаковые значения при
n+1 различном значении буквы
x, то они равны тождественно.
Второе утверждение легко доказать. Составим разность
H(x)=F(x)–G(x). Степень многочлена
H(x) не больше
n. С другой стороны, в тех точках, где значения
F(x) и
G(x) одинаковы, многочлен
H(x) обращается в
0. Если таких чисел больше
n, то многочлен
H(x) тождественно равен нулю, т. е.
F(x)=G(x), что и требовалось доказать.
Теорема о тождестве позволяет доказывать тождество не преобразованиями,
а подстановкой конечного числа значений букв.
|
|
Пример.
Доказать тождество.
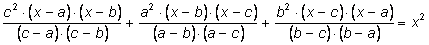
В двух частях стоят многочлены второй степени. Для доказательства
тождества достаточно подобрать три различных значения
x, для которых совпадут значения слева и справа.
1.
x=a. Слева останется одно среднее слагаемое,
равное
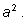Справа также будет
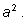
2, 3.
x=b;
x=c – вычисления аналогичны.
Тождество доказано. |
| |