Нахождение корней многочлена – интересная и
достаточно трудная задача, решение которой выходит за границы
школьного курса математики. Однако для многочленов с целыми
коэффициентами есть простой переборный алгоритм, позволяющий находить
все рациональные корни. |
Теорема. Если многочлен с целыми
коэффициентами имеет рациональный корень
(
–
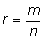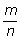несократимая дробь),
то числитель дроби является делителем свободного члена, а
знаменатель – делителем старшего коэффициента этого многочлена. |
Доказательство
Пусть многочлен записан в каноническом виде
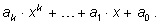Подставим
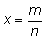и освободимся от знаменателей, домножив на наибольшую
степень n:
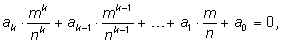
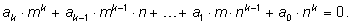
Перенесем вправо член
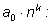
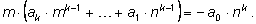
Произведение
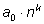делится на целое число m. По условию дробь
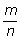несократима, следовательно, числа m и n взаимно просты. Тогда взаимно
простыми будут числа m и
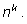Если произведение чисел
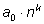делится
на m, а множитель
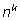взаимно прост с m, то второй множитель
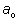должен
делиться на m.
Доказательство делимости старшего коэффициента
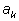на знаменатель n доказывается точно так же, перенося вправо член
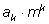и вынося слева
множитель n за скобку.
Сделаем несколько замечаний к доказанной теореме.
Замечания
1) Теорема дает только необходимое условие существования рационального
корня. Это означает, что нужно проверить все рациональные числа, с
указанным в теореме свойством и отобрать из них те, которые окажутся
корнями. Других не будет.
2) Среди делителей надо брать не только положительные, но и
отрицательные целые числа.
3) Если старший коэффициент
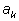равен 1, то всякий рациональный корень
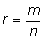должен быть целым, так как у 1 нет
делителей, кроме
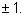
Проиллюстрируем теорему и замечания к ней на примерах. |
Примеры.
1)
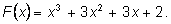Рациональные корни должны быть целыми.
Перебираем делители свободного члена:
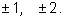Положительные числа
подставлять нет смысла, так как все коэффициенты многочлена
положительны и
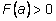при
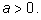
Осталось вычислить F(–1) и F(–2). F(–1)=1+0; F(–2)=0.
Итак, многочлен имеет один целый корень x=–2.
Можем поделить F(x) на x+2 :
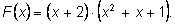
2)
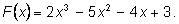Выписываем возможные значения корней:
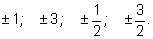
Подстановкой убеждаемся, что
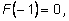
и
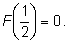Многочлен
имеет три различных рациональных корня:
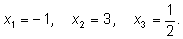
Конечно, корень x = -1 угадывается легко. Потом можно разложить на
множители
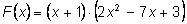и искать корни квадратного
трехчлена
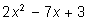обычными приемами. |
Упражнение. Найти целые корни
многочлена, используя сформулированную выше теорему:
x7 + 10x6-371x5 - 890x4 + 38875x3 - 107282x2 - 369705x + 882882 |
Указание. Для
разложения свободного члена на множители используйте инструмент
деления с остатком (верхний инструмент).
Для проверки корней используйте схему Горнера
(инструмент слева внизу).
Для хранения промежуточных и итоговых результатов
(множителей свободного члена и корней многочлена) используйте ячейки справа внизу
(перемещать в них числа из окна инструментов и обратно или прямо со страницы можно простым "перетягиванием мышкой" с
предварительным выделением числа мышкой). |
|
| |