|
Многочлены от двух переменных
Возьмем две буквы
x и
y. Произведение
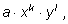 где
а – число, называется одночленом. Его степень
равна
k+l. Сумма одночленов называется многочленом. В
отличие от многочленов с одной переменной, для многочленов с большим
числом переменных нет общепринятой стандартной записи.
где
а – число, называется одночленом. Его степень
равна
k+l. Сумма одночленов называется многочленом. В
отличие от многочленов с одной переменной, для многочленов с большим
числом переменных нет общепринятой стандартной записи.
Так же, как и многочлены от одной переменной, многочлены от двух
переменных могут раскладываться на множители. Важным разложением
является разложение разности n-ых
степеней, которое вам известно для
n=2 и
3:
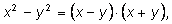
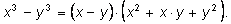
Эти формулы легко обобщаются для произвольного
n:
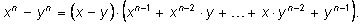
Сумма
n-ых степеней легко раскладывается в случае,
когда
n нечетно. Слагаемое
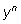 можно представить в виде
можно представить в виде
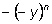 и воспользоваться формулой разложения разности
n-ых степеней.
и воспользоваться формулой разложения разности
n-ых степеней. |
Пример.
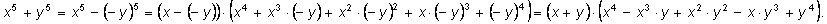 Это тождество проверяется прямым перемножением скобок правой части. |
Симметричные многочлены
Среди многочленов от двух переменных важную роль играют симметричные
многочлены, т. е. многочлены, не меняющиеся при перестановке букв
x и
y. |
|
Примеры
симметричных многочленов
0) 1;
1)
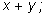
2)
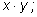
3)
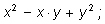
4)
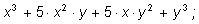
5)
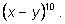
Первые три многочлена называются основными:
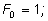
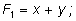
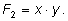 Их роль состоит в том, что любой симметричный многочлен
от двух переменных может быть выражен через
Их роль состоит в том, что любой симметричный многочлен
от двух переменных может быть выражен через
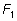 и
и
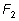 с помощью операция сложения и умножения.
с помощью операция сложения и умножения. |
|
Рассмотрим в качестве примера разложение суммы степеней
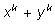 через суммы через суммы
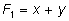 и произведение и произведение
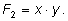
Пусть
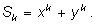 Умножим Умножим
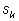 на на
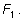 Так как Так как
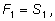 то то
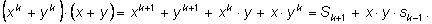
Получаем тождество
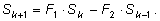 Зная Зная
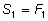 и
и
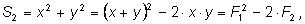 мы последовательно сможем вычислить мы последовательно сможем вычислить
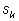 для любого
k.
для любого
k.
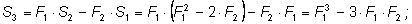
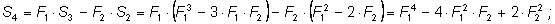
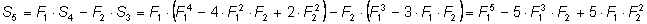 и т. д.
и т. д.
С помощью теоремы Виета мы можем выразить любой симметричный многочлен
от корней
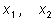 квадратного трехчлена квадратного трехчлена
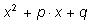 через коэффициенты
p и
q, так как через коэффициенты
p и
q, так как
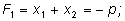 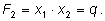
Например, найдем
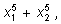 где где
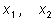 – корни трехчлена
– корни трехчлена
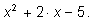 Воспользуемся полученной ранее формулой для суммы
5-ых степеней: Воспользуемся полученной ранее формулой для суммы
5-ых степеней:
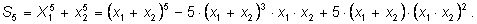 По теореме Виета По теореме Виета
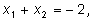 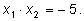 Подставляя, получим
Подставляя, получим
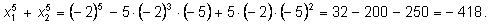
От Ньютона идет другой способ решения этой (и аналогичной ей) задачи
без использования формулы для
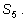 Подставим корни
Подставим корни
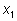 и
и
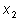 в уравнение.
Получим равенства
в уравнение.
Получим равенства
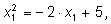
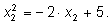
Сложим:
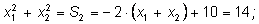
умножим равенства на
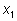 и
и
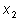 и сложим:
и сложим:
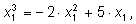
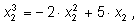
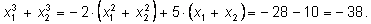
Продолжаем аналогично:
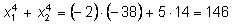
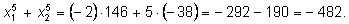
Многочлены от нескольких переменных
Аналогично случаю двух переменных можно строить многочлены от любого
числа переменных. Выберем
m букв
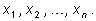 Построим одночлены
Построим одночлены
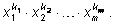 Многочлен – это сумма таких одночленов, снабженных
числовыми коэффициентами.
Многочлен – это сумма таких одночленов, снабженных
числовыми коэффициентами.
Приведем несколько тождеств, в которых участвуют многочлены от
нескольких переменных.
1)
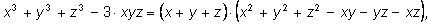
2)
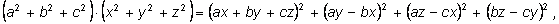
3)
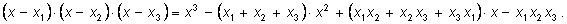 |
|
Степенью одночлена называется сумма степеней,
с которыми в него входят все буквы.
Степенью многочлена называется наибольшая степень одночлена,
входящего в этот многочлен (с ненулевым коэффициентом). |
|
В первом из наших примеров в левой части стоит
многочлен третьей степени с тремя переменными (буквами
x, y и
z ). Во втором – многочлен четвертой степени с шестью
буквами
a, b, c, x, y, z. В
третьем – многочлен третьей степени с четырьмя буквами
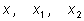 и
и
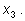 |
| Многочлен называется однородным,
если все его одночлены имеют одну и ту же степень. В наших примерах
все многочлены были однородными. |
|
Среди многочленов с несколькими буквами большую
роль играют симметричные (или симметрические) многочлены. В наших
примерах первые два многочлена были симметричными. Как и в случае двух
переменных, можно выделить основные симметричные многочлены:
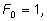 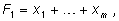
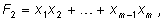

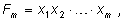 где
где
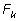 представляет собой сумму
всевозможных произведений, взятых по
k букв
из данных
m букв.
представляет собой сумму
всевозможных произведений, взятых по
k букв
из данных
m букв.
Аналогично случаю двух букв каждый симметричный многочлен может быть
представлен как многочлен от основных симметричных многочленов. |
Например, тождество
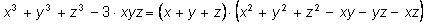
можно преобразовать так:
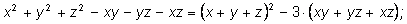
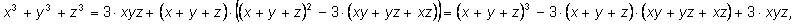
т. е.
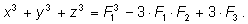 |
|
Одним из наиболее
известных многочленов двух переменных является бином Ньютона -
разложение степени двучлена
(ax + by)n
в сумму одночленов. Бином Ньютона подробно будет изучаться в теме
"Комбинаторика". Здесь же рассмотрим несколько упражнений, связанных
с определением двучлена и упорядочиванием одночленов в представлении
многочленов. |
|
Упражнения.
Ниже приведены простые инструменты для получения требуемых
одночленов в разложении бинома. Для работы с инструментом надо
указать сначала степень многочлена (бинома), затем степень
x в разложении. При этом автоматически
будет вычислена степень
y. Далее нужно ввести коэффициенты при
x и
y, справа появится выражение для выбранного
одночлена в разложении бинома.
1. Найдите первый и последний члены
биномов
(4x + 3y)5,
(5x - 2y)5.
2. Определите наибольшие по абсолютной
величине коэффициенты в каждом разложении. Для каких степеней
одночленов они получаются? |
|
|
| |