|
Исторические сведения о многочленах
До середины XIX века центральной задачей алгебры было нахождение
формулы для корней уравнения
P(x) = 0, где
P – многочлен произвольной степени. Эта задача
была полностью решена в работах молодых математиков первой трети XIX
века – Э. Галуа (1811–1832), Н. Абеля (1802–1829) и П. Руффини
(1765–1822).
|
Галуа |
|
Эварист |
|

|
|
Годы жизни:
|
|
1811-1832 |
Еще в XVI веке итальянскими математиками были найдены формулы для
решения уравнений третьей и четвертой степени. Абель и Руффини
доказали, что, начиная с пятой степени, общей формулы, использующей,
кроме сложения и умножения, лишь извлечение корней, не существует, а
Галуа открыл закономерности поведения корней, приложимые к каждому
конкретному уравнению.
Параллельно с этим К. Гаусс доказал основную теорему алгебры,
утверждающую, что всякий многочлен (коэффициенты многочлена могут быть
не только вещественными, но и комплексными числами) имеет хотя бы один
корень (возможно, являющийся не вещественным, а комплексным числом).
После этого вопрос о вычислении корней многочлена переместился из
алгебры в теорию функций и приближенных вычислений.
В XX веке роль многочленов стала меняться. Буквы, входящие в
многочлен, все больше стали играть роль символов, не связанную с их
конкретными значениями. Самые разные области математики и ее
приложений стали использовать символьное исчисление многочленов, не
зависящее от теории функций (математическая логика, топология, теория
информации, дискретная и компьютерная математика и т. д.).
Приведем
пример. В XX веке важнейшей задачей человечества стала задача передачи
информации (радио, телефон, передача видеосигналов
и т. д.).
|
Абель |
|
Нильс Хенрик |
|

|
|
Годы жизни:
|
|
1802-1829 |
Математически сообщение может быть записано в виде
последовательности символов (точки и тире в старинной азбуке Морзе,
нули и единицы и т. п.), передаваемой по так называемому каналу связи
(например, в виде радиосигналов). При передаче возможны искажения,
которые при приеме сообщения должны быть исправлены. Была предложена
(и активно используется по настоящее время) идея кодирования сообщения
– такой его передачи, что после приема-передачи можно было бы
обнаружить и исправить случайные ошибки. Основной способ кодирования
состоит в следующем. Из последовательности сигналов (например, из цифр
0 и
1 )
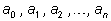 составляется формальный многочлен
составляется формальный многочлен
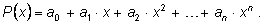 Затем подбирается некоторый фиксированный многочлен
Q(x) (кодирующий многочлен) и умножается на
P(x). Передается не исходная последовательность сигналов, а
последовательность коэффициентов произведения
Затем подбирается некоторый фиксированный многочлен
Q(x) (кодирующий многочлен) и умножается на
P(x). Передается не исходная последовательность сигналов, а
последовательность коэффициентов произведения
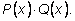 Многочлен
Q(x) можно подобрать так, что при приеме будут
распознаваться случайные ошибки, возникшие при передаче. При этом
поиск кодирующего многочлена
Q(x) оказался чисто алгебраической задачей, так
как эта задача связана с вопросами делимости многочлена и поведения
его корней.
Многочлен
Q(x) можно подобрать так, что при приеме будут
распознаваться случайные ошибки, возникшие при передаче. При этом
поиск кодирующего многочлена
Q(x) оказался чисто алгебраической задачей, так
как эта задача связана с вопросами делимости многочлена и поведения
его корней.
Определение многочлена |
Одночленом от
некоторой буквы
x называется алгебраическое выражение
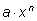 ,
где
a – некоторое число,
x – буква,
n – целое неотрицательное число. Одночлен ,
где
a – некоторое число,
x – буква,
n – целое неотрицательное число. Одночлен
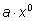 отождествляется с числом
a, т.е. числа мы можем рассматривать как
одночлены.
отождествляется с числом
a, т.е. числа мы можем рассматривать как
одночлены. |
Одночлены называются
подобными, если показатели степени у буквы одинаковы. Подобные
одночлены можно складывать по правилу:
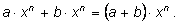
Это действие называется приведением подобных членов. |
|
Многочленом называется алгебраическая сумма
одночленов. |
|
Любой многочлен от одной буквы
x (ее часто называют переменной) после приведения
подобных членов может быть записан по убывающим степеням этой буквы в
виде
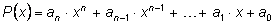 или по возрастающим степеням
или по возрастающим степеням
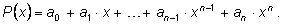
Такая запись многочлена называется канонической. |
Если
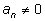 ,
то число
n называют степенью многочлена, коэффициент ,
то число
n называют степенью многочлена, коэффициент
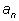 – старшим коэффициентом. Коэффициент
– старшим коэффициентом. Коэффициент
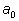 называют свободным членом. Константу
называют свободным членом. Константу
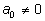 считают многочленом степени
0, нулевому многочлену степень не приписывается.
Степень многочлена
P будем обозначать так:
deg P.
считают многочленом степени
0, нулевому многочлену степень не приписывается.
Степень многочлена
P будем обозначать так:
deg P. |
Если на многочлен смотреть
как на символическое выражение, то возникает естественный вопрос, что
означает, что два многочлена равны между собой? Слово «равенство»
используется в двух разных смыслах.
Алгебраический смысл равенства многочленов: два многочлена
равны, если они состоят из одних и тех же одночленов.
Для проверки равенства многочленов надо сравнить коэффициенты при
подобных одночленах. В частности, если многочлен содержит только одну
букву, то надо сравнить коэффициенты при одинаковых степенях этой
буквы. |
|
Например, алгебраическое равенство многочленов от
x 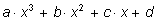 и
и
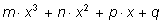 означает равенство коэффициентов:
a=m, b=n, c=p, d=q.
означает равенство коэффициентов:
a=m, b=n, c=p, d=q. |
|
Тождественный смысл равенства
многочленов: многочлены равны, если равны их значения при всех
значениях входящих в этот многочлен букв.
Проверить тождественное равенство многочленов по такому определению
невозможно, так как пришлось бы подставлять бесконечное число значений
букв и на это не хватило бы целой жизни.
Какова же связь между понятиями алгебраического и тождественного
равенства многочленов?
В одну сторону связь очевидна: если многочлены равны алгебраически, то
они равны и тождественно, так как оба многочлена состоят из одних и
тех же членов, и, подставляя в них любые значения букв, мы будем иметь
совпадающие числовые выражения.
Доказать обратное утверждение, т. е. что из тождественного равенства
многочленов следует их алгебраическое равенство, нелегко. В основе
этого факта лежит замечательное утверждение о многочленах от одной
буквы. |
| Теорема о тождестве.
Для алгебраического равенства двух многочленов от одной
буквы достаточно проверить равенство значений двух многочленов,
подставляя вместо букв числа в количестве, большем, чем степень этих
многочленов. |
| Например, два многочлена
первой степени совпадают, если равны их значениях при двух значениях
буквы; для квадратных многочленов достаточно проверить совпадение
значений при трех значениях буквы; для кубических – при четырех и т.
д. |
| |