|
Извлечение корня – это операция, обратная операции
возведения в степень.
Пусть n – натуральное число,
большее единицы. |
|
Корнем n-й степени из числа а
называется такое число
b, n-я степень которого равна
а, т. е.
b – корень
n-й степени из
 |
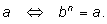Можно сказать иначе, что корень
n-й степени из числа
а – это всякий корень уравнения
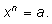Поэтому выяснить, существует ли корень
n-й степени для данного числа (и если он есть, то один
или их несколько), можно, решив уравнение
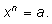Ответ на этот вопрос зависит от значений чисел
n и
а и от того, какие корни, т. е. какие значения
х, нас интересуют.
Следующая теорема утверждает существование и единственность
положительного корня
n-й степени из положительного числа. На ней
основано введение новой операции – извлечение корня
n-й степени, а также использование радикалов. |
|
Теорема.
Пусть
n — натуральное число. Для всякого
неотрицательного числа
а существует неотрицательное решение уравнения
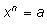и такое решение единственно. Это решение называется арифметическим корнем
n-ой степени из числа
a и обозначается значком радикала
 |
|
|
|
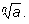Упражнения. Используя
инструмент динамического рисунка, выполните следующие задания.
а) Решите уравнения
x7=2187;
x20=1048576;
б) Проследите за изменением арифметического корня
степени
n из числа
n при росте
n.
Выдвиньте гипотезу о характере изменения этого корня. |
Ответ на вопрос о существовании и количестве решений уравнения
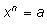для отрицательных значений
а зависит от чётности или нечётности числа
n.
1) Пусть
n – нечетное число. Тогда для любого числа
уравнение
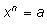имеет единственное решение. Другими
словами, если
n нечетно, то при любом значении
а существует единственный действительный корень
из числа
а. Он также обозначается с помощью знака радикала:
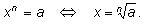Тем самым, для нечётных значений п под
радикалом может стоять отрицательное число. Нетрудно проверить, что
для нечётных
n верно следующее:
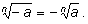
2) Пусть
n – четное число. Если
а<0, то уравнение
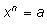корней не имеет, потому что квадрат, а
следовательно, и любая четная степень числа будет положительным (или
равным нулю) числом.
Пусть теперь
а>0. Сначала заметим, что если
х – корень уравнения
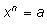при четном
n (
n=2k ), то и число
–х является его корнем, так как
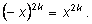Следовательно, в этом случае уравнение
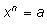имеет два действительных решения – они равны по модулю и
противоположны по знаку.
В то же время положительный корень уравнения
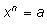при четном
n и
а>0 является единственным, он также обозначается
с помощью радикала: (
n – четно и
а>0 ) – это число
b такое, что
b>0 и
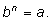Соответствующий отрицательный корень записывается так:
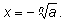
Таким образом,
(
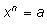n – четно и
а>0 )
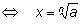или
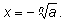
Итак, запись
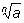имеет смысл:
при нечетном
n для любого а и обозначает единственный существующий
корень
n-й степени из
а;
при четном
n только для
а>0 и обозначает единственный неотрицательный корень
n-й степени из
а. |
Примеры решения простейших уравнений
1)
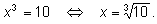
2)
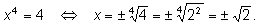
3)
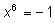–вещественных корней нет. |
| |