| |
| Основные свойства арифметических корней.
Будем считать, что все рассматриваемые числа неотрицательны, а числа,
стоящие в знаменателе, не равны нулю.
Свойство 1.
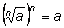 .
.
Свойство
2.
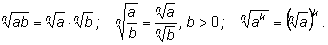
Свойство
3.
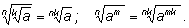
Свойство 4. Если а > b, то
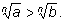
Свойство
5. Пусть m > n. Если а > 1, то
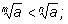 если 0 < а < 1, то
если 0 < а < 1, то
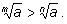
|
Замечание. Некоторые формулы с небольшими изменениями можно
переписать и для отрицательных чисел. При этом под знаком радикала
может появится модуль числа.
Например, если числа а и b одного знака, свойство 2
запишется так:
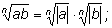
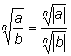
|
| Упражнение 1.
|
Испытайте на
примере свойство 2 (первое равенство). Для этого рассмотрите пример: n = 3, a = 2197, b = 4913.
Указание. На инструменте слева вычислите корень третьей
степени из a. На среднем
инструменте - корень третьей степени
из b. На правом нужно вычислить корень третьей степени из
произведения a на b. Разумеется, после вычисления первых двух
корней вам будет известен ответ 221, однако перемножить устно числа a и b трудно (а считать на
калькуляторе неинтересно).
Попробуйте найти это произведение методом последовательных
приближений (например, методом половинного деления:
"перелёт"-"недолёт" для угадывания цифр, начиная
со старшего разряда к младшему). Сколько раз вам пришлось вычислить корень? |
| |
|
Испытайте на
примере свойство 3 (первое равенство). Для этого рассмотрите пример: n = 7, k = 8, a = 1679616.
Указание. На инструменте слева вычислите корень k-ой степени из a. На среднем
инструменте - корень n-ой степени
из результата. На правом нужно вычислить корень степени nk из a. Сравните результаты на среднем
и правом инструментах. |
| Доказательство всех свойств
проводится по одной и той же схеме. Докажем, например, первые из
свойств 2 и 3. |
Доказательства
свойств корней.
Свойство 2.
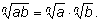
По определению
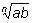 – это такое число, n-я степень
которого равна аb. Если n –четное
число, то это число положительно.
Проверим, что этим же свойством обладает правая часть.
– это такое число, n-я степень
которого равна аb. Если n –четное
число, то это число положительно.
Проверим, что этим же свойством обладает правая часть.
Возведем ее в n-ю степень:
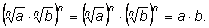 При четном n каждый
множитель
При четном n каждый
множитель
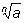 и
и
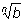 положителен, поэтому произведение
положителен, поэтому произведение
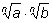 положительно.
положительно.
Свойство 3.
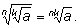 Возведем
число
Возведем
число
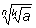 в степень nk:
в степень nk:
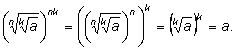 Это означает, что
Это означает, что
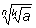 – корень степени nk из числа a. Если число nk четно, то, по условию, число a положительно, а тогда
являются положительными числа
– корень степени nk из числа a. Если число nk четно, то, по условию, число a положительно, а тогда
являются положительными числа
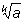 и
и
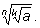
|
Примеры преобразований дробных выражений с корнями
1)
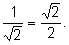
2)
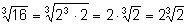 и т.д.
и т.д.
3)
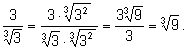
4)
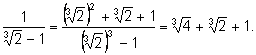
5)
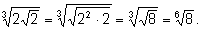
6)
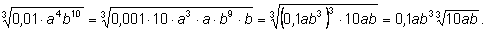
|
| |
Примеры и
комментарии об операциях с радикалами
Замечание 1. Выражение
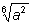 имеет смысл при любом значении a, так как под корнем стоит выражение
имеет смысл при любом значении a, так как под корнем стоит выражение
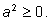 Однако при сокращении показателей надо учесть знак a: если
Однако при сокращении показателей надо учесть знак a: если
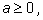 то
то
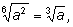 если же
если же
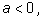 то
то
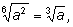 например,
например,
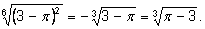
Замечание 2. Выражение
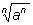 при четном n имеет смысл при любом значении a. При этом если
при четном n имеет смысл при любом значении a. При этом если
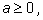 то
то
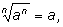 если же
если же
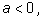 то
то
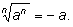 Последние два случая можно объединить:
Последние два случая можно объединить:
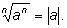
Аналогично, при нечётном n верна формула
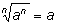 при любом значении a.
при любом значении a.
Объединив вместе оба случая чётности n получим:
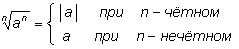
Замечание 3. Запись корней в удобной форме.
Иногда бывает удобно убрать корень из знаменателя или вынести
множитель из-под корня.
Замечание 4. Преобразования выражений с радикалоами.
Часто при решении задач приходится, упрощая выражение, извлекать
корень частично, т.е. не из всего выражения, а только из его части,
избавляться от корней в числителе или знаменателе, приводить корни к
одному показателю корня и совершать другие действия, которые помогут
произвести дальнейшие преобразования. Избавляясь от корня в числителе
или знаменателе, мы умножаем числитель и знаменатель на такое
выражение, чтобы извлекся корень, от которого мы хотим избавиться. |
| |
Примеры преобразования радикалов
1)
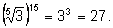
2)
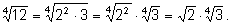
3)
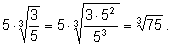
4)
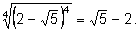
5)
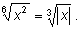
|
| |
Примеры на сравнение чисел, записанных с помощью радикалов
1)
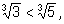 так как
так как
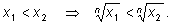
2)
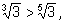 так как
так как
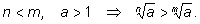
3)
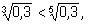 так как
так как
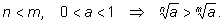
|
| |