Исторические сведения
Как построить квадрат, равновеликий данному прямоугольнику? На современном алгебраическом языке для этого надо решить уравнение 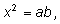   где  a  и  b  – стороны прямоугольника, а  x  – неизвестная сторона квадрата. Геометрически надо построить отрезок  x,  исходя из пропорции  

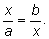
И в алгебраической, и в геометрической постановке эту задачу научились решать несколько тысяч лет назад. Слово «квадратный корень» математики древности еще не употребляли, но умели вычислять квадратный корень с любой степенью точности.
Одновременно с решением практических задач, требующих «извлечения корня», постановка вопроса о решении уравнения типа 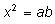  привела древнегреческих математиков к открытию иррациональных чисел. Они доказали, что нельзя найти общую меру для стороны квадрата и его диагонали, что на языке алгебры означает, что число 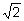   не является рациональным.
Как построить куб, объем которого вдвое больше объема данного куба? Уже эту задачу, которая сводится к извлечению кубического корня из двух, греки решить не смогли, и она осталась в наследство математикам нового времени как одна из знаменитых нерешенных задач древности. Легенда связывает ее с мифом о предсказании оракула: чтобы избавиться от жестокого мора, необходимо удвоить священный жертвенник на острове Делос, имеющий форму куба.

На самом деле математики древней Греции предложили много способов решения этой задачи. Например, Менехм (III в. до н. э.) заметил, что извлечение кубического корня из числа 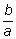   можно выполнить, найдя два средних пропорциональных, т. е. решив такую пропорцию: 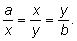   Эта пропорция сводится к системе 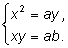   Следствием этой системы будет равенство  

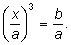
Для решения системы Менехм предложил искать точку пересечения параболы 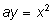   и гиперболы 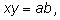   хорошо известных к тому времени кривых. Неудовлетворительность решения Менехма состояла в том, что пришлось придумать устройства (кстати, очень простые и удобные) для нахождения точки пересечения параболы и гиперболы, а разрешалось пользоваться лишь циркулем и линейкой. Невозможность построения кубического корня с помощью циркуля и линейки (и тем самым невозможность классического решения делосской задачи об удвоении куба) была доказана лишь в XIX веке.

Решение различных задач, связанных с построением кривых, задаваемых алгебраическими уравнениями, привело к широкому использованию того, что мы сейчас называем корнями  n-ой степени. Было открыто много способов и формул для приближенного вычисления корней, хотя образ «извлечения корня» сохранился до наших дней как символ бессмысленного труда математика-профессионала.
Если необходимость совершать обратную операцию к операции возведения в n-ую степень, была осознана достаточно давно, то задача нахождения показателя степени по заданному результату, т. е. задача решения уравнения  a^x  = b  стала интересной лишь в XVII веке.
Эта задача была тесно связана с необходимость быстро производить громоздкие вычисления. Идея упрощения вычислений, которая привела к изобретению логарифмов, состояла в сравнении поведения степеней и показателей при умножении, делении, возведении в степень и извлечении корня. С помощью таблиц, сопоставляющих степени и показатели, можно было заменить умножение сложением, а возведение в степень умножением. Соответствующие подробные таблицы были составлены в конце XVI – начале XVII века, а сам термин «логарифм» был введен автором самых совершенных таблиц того времени, шотландцем Д. Непером в 1614 году. Как сказал французский математик П. Лаплас, «изобретение логарифмов, сократив работу астрономов, продлило им жизнь». К этому стоит добавить, что сам Непер был любитель-астроном и составлял свои таблицы для обработки результатов астрономических наблюдений.
 

Все таблицы логарифмов до 1950 г. являлись перепечаткой или сокращением таблиц Бриггса. Генри Бриггс (1561-1630) с очень большой точностью (16  знаков после запятой) извлек подряд  57  квадратных корней из  10  и получил значения  
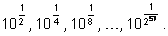
Комбинируя эти значения, он получил густую сетку чисел с известными десятичными логарифмами: 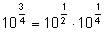   и т.п. После этого десятичный логарифм любого числа x из промежутка  [1;10]  с хорошей точностью находится округлением до ближайшего известного.
Это огромная работа, и за 300 лет не нашлось никого, кто повторил бы ее. Немного раньше Бриггса таблицу натуральных логарифмов составил Джон Непер (1550 – 1617).

С появлением компьютера ситуация переменилась. Умножение по-прежнему выполняется дольше, чем сложение, но логарифмирование требует еще больше времени. Поиск числа в таблице – очень дорогая операция для компьютера. Поэтому теперь значение логарифмов как инструмента вычисления резко упало, а с распространением калькуляторов оно сходит на нет. С другой стороны, сами по себе логарифмические зависимости легко обрабатываются и используются при вычислениях на компьютере. Например, формула  a^x = exp (x ln a)  (кроме  к = 1, 2, 3 ) служит основным средством возведения в степень на всех компьютерах и калькуляторах. На современных компьютерах (и на калькуляторах) значения логарифмов вычисляют, пользуясь заранее найденными приближенными формулами. По этим формулам вычисление логарифмов становится довольно простым. Пользователю компьютера никогда не приходится думать о вычислении логарифмов: на всех компьютерах для этого имеются стандартные программы.