Определение степени с рациональным показателем |
Пусть a>0, r – рациональное число.
Запишем r в виде дроби со знаком:
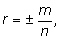где
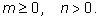
Определим
|
|
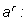
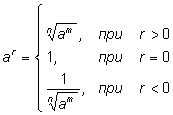
Динамическая иллюстрация степени с дробным показателем
|
Упражнения. Испытайте
инструмент возведения в дробную степень:
1. Возведите 625 в степень 1/4.
2. Разделите 1 на 5 в седьмой степени.
3. Найдите корень степени 4 из 4096.
4. Найдите корень восьмой степени от числа 6561, возведённого в седьмую степень.
5. Найдите число, обратное к корню седьмой степени из куба числа 78125. |
| |
Примеры
1)
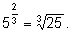
2)
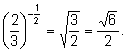
3)
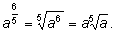
4)
|
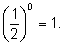
Замечание.
Заметим, что, хотя запись
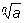при нечетном n определена и при a<0, степень с дробным показателем мы
используем только для a>0 Иными словами, запись
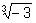возможна, а запись
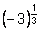нет. Это связано с тем, что запись рационального числа в
виде дроби неоднозначна. Например,
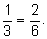Степен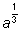и
и
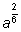должны быть одним и тем же числом, так как показатели
равны, хотя и записаны по-разному. Если бы определение степени мы
приложили к числу а=–3, то получили бы противоречие:
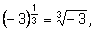но
|
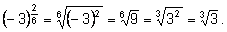
Свойства степени с
рациональным показателем
1)
|
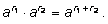
2)
|
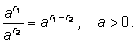
3)
|
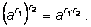
4)
|
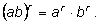
5)
|
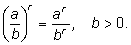
6)
|
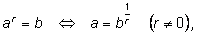
7)
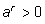при любом рациональном r,
|
8) пусть
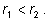Если a>1, то
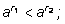если 0<a<1, то
|
|
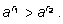
Примеры доказательства свойств степени с рациональным показателем
Свойство рациональной степени |
Доказательство на основе свойств
радикалов |
Примечание |
|
|
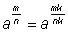
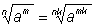
Свойство независимости дробной
степени от выбора представления показателя. Доказано для
положительных показателей. |
|
|
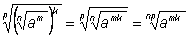
Возведение степени в степень.
Доказано для положительных показателей. |
| |
|
|
|
|
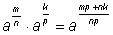
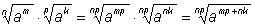
Произведение степеней с одинаковыми
основаниями. Доказано для положительных показателей. |
|
|
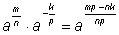
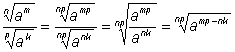
Произведение степеней с одинаковыми
основаниями. Доказано для одного положительного, другого –
отрицательного показателей. |
|
|
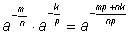
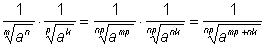
Произведение степеней с одинаковыми
основаниями. Доказано для отрицательных показателей. |
|
Примеры
Приведение степеней к одному основанию (в данном случае, к основанию
2).
1)
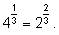
2)
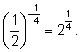
3)
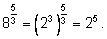
4)
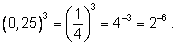
Действия над степенями
1)
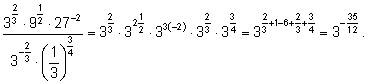
2)
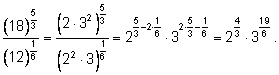
3)
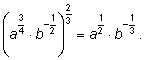
4)
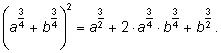
Решение простейших уравнений.
1)
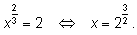
2)
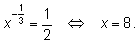
3)
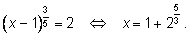
Сравнение степеней.
1)
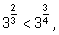так как
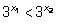при
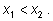
2)
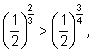так как
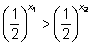при
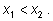
3)
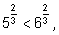так как
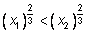при
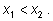
4)
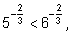так как
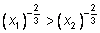при
|
| |
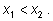