|
Определение степени с действительным показателем
Можно определить степень
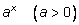 не только для рационального, но и для любого действительного показателя
x. Для этого рассматривают последовательность
рациональных приближений к числу
x, т. е. последовательность рациональных чисел
не только для рационального, но и для любого действительного показателя
x. Для этого рассматривают последовательность
рациональных приближений к числу
x, т. е. последовательность рациональных чисел
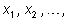 которые задают число
x с любой степенью точности. Затем вычисляют
степени с рациональными показателями
которые задают число
x с любой степенью точности. Затем вычисляют
степени с рациональными показателями
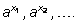 Оказывается, что эти числа являются приближениями к некоторому числу
y, причём, уточнением рационального приближения
числа
x можно добиться вычисления
Оказывается, что эти числа являются приближениями к некоторому числу
y, причём, уточнением рационального приближения
числа
x можно добиться вычисления
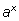 с любой степенью точности. Это число и считают степенью
с любой степенью точности. Это число и считают степенью
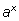 с показателем
x.
с показателем
x. |
|
Свойства степени с действительным
показателем
На степени с действительными показателями переносятся все свойства
степеней с рациональными показателями.
1)
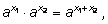
2)
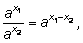
3)
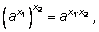
4)

5) 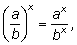
6)
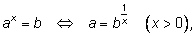
7) 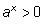 при любом действительном
x,
при любом действительном
x,
8) пусть 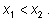 Если
Если 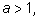 то
то 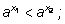 если
если 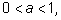 то
то 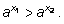
Основания степеней везде считаются положительными. |
|
Доказательство свойств степени с произвольным
действительным показателем проводится, на основе использования перехода
к пределу в свойствах степеней с рациональным показателем и связана с
более глубоким изучением понятия действительного числа.
Предельный переход будет обсуждаться позднее. |
|
Упражнения.
1. Используя встроенный в страницу калькулятор, вычислите
приближённо степени
с действительным показателем:
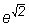 , ,
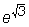 , ,
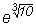
(здесь
e = 2,718281828459... - иррациональное число, введённое
Эйлером, которое будет изучаться позже,
exp (x) = ex
).
2. Вычислите
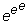 .
Сравните результат с .
Сравните результат с
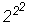 и и
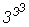 .
Велика ли погрешность? .
Велика ли погрешность? |
|
|
| |