|
Определение логарифма. Пусть
a > 0,
x – любое действительное число.
Мы знаем, что
существует степень числа
а с показателем
x, т. е. число
b = ax
Это число
b всегда будет положительным.
В записи числа
b
= ax
число
а называют основанием,
x – показателем степени,
b – степенью.
Среди оснований
а есть одно исключительное основание
a = 1. Любая степень этого основания равна
1 :
11 =
1
Если же
a
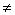 1,
то степени
ax
будут различны при различных показателях, и мы сможем определить
показатель x
из равенства
ax
= b
|
|
Логарифмом числа
b по основанию
a
называется показатель степени,
в которую надо возвести
a,
чтобы получить число
b.
|
|
В качестве основания мы будем всегда брать положительное число
a, отличное от
1.
|
|
|
|
|
|
Упражнение.
Используя инструмент вычисления логарифма, найдите следующие
показатели степени. Используя определение логарифма дайте
обоснование полученным результатам. Перед вычислениями сделайте
прогноз относительно результата по двум параметрам: больше или
меньше нуля показатель, и превышает ли он единицу по абсолютной
величине.
1) Определить, в какую степень надо возвести число
2, чтобы получить
1048576.
2) Определить, в какую степень надо возвести число
7, чтобы получить
40353607.
3) Определить, в какую степень надо возвести число
0.5, чтобы получить
0.03125.
4)
Определить, в какую степень надо возвести число
5, чтобы получить
0.0000128.
5) Определить, в какую степень надо возвести число
0.00390625, чтобы получить
2. |
|
В записи
b = ax
число x
- это показатель степени, в которую надо возвести основание
a,
чтобы получить число
b. Следовательно,
x
- это логарифм числа
b по основанию
a:
x = loga b. |
|
Формулы
ax
= b и
x = logab.
равносильны,
то есть выражают одну и ту же связь между
числами a,
x
и
b (при
a
> 0, a
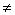1,
b > 0).
|
|
Основное логарифмическое тождество
Подставляя в равенство
ax
= b запись числа x
в виде логарифма, получаем равенство, называемое основным
логарифмическим тождеством:
|
 |
|
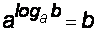Представляя в равенстве
x
= loga b
выражение
b в виде степени, получим ещё
одно тождество:
x = loga ax |
| |