Мы можем встретить в вычислительных задачах степени
различных чисел в разных сочетаниях, например, при вычислении
выражения
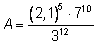 надо возводить в степень разные числа, умножать и делить
степени. Зачем так много степеней? Нельзя ли обойтись степенями
какого-то одного основания? Конечно, можно.
надо возводить в степень разные числа, умножать и делить
степени. Зачем так много степеней? Нельзя ли обойтись степенями
какого-то одного основания? Конечно, можно.
Первое правило
Можно выбрать одно удобное основание, например а, и привести любую степень к основанию а, то есть представить любую степень
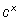 в виде
в виде
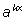 при некотором k. Этот коэффициент k и есть логарифм:
при некотором k. Этот коэффициент k и есть логарифм:
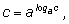 поэтому, обозначая
поэтому, обозначая
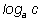 через k, мы получим:
через k, мы получим: |
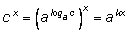
|
Это правило позволяет пользоваться каким-то одним
основанием. В одних задачах удобно брать
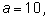 в других (особенно дискретных задачах) – брать
в других (особенно дискретных задачах) – брать
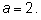 Для вычисления приведенного выше выражения А с помощью калькулятора, умеющего вычислять
Для вычисления приведенного выше выражения А с помощью калькулятора, умеющего вычислять
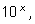 надо все привести к степени 10 :
надо все привести к степени 10 :
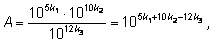 где
где
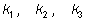 – логарифмы чисел 2,1; 7 и 3 по основанию 10. Внимательный человек может дополнительно
заметить, что
– логарифмы чисел 2,1; 7 и 3 по основанию 10. Внимательный человек может дополнительно
заметить, что
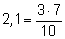 и сделать упрощения:
и сделать упрощения:
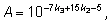 избавившись от логарифма числа 2,1.
избавившись от логарифма числа 2,1.
Второе правило
При логарифмировании можно также выбрать одно удобное основание и
сводить все логарифмы к этому основанию. Для этого существует
специальная формула, которую мы сейчас выведем.
Пусть мы хотим перейти от логарифмов по основанию а к логарифмам по другому основанию b. Запишем основное логарифмическое тождество:
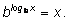
Прологарифмируем его по основанию а :
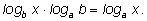
Получаем: |
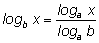
|
Эту формулу часто читают так: логарифм числа по
новому основанию равен логарифму числа по старому основанию, деленному
на логарифм нового основания по старому основанию.
Выведенную формулу называют формулой перехода от одного основания
логарифма к другому.
Таким образом, мы видим, что при изменении основания значения
логарифмов изменяются пропорционально:
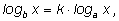 где
где
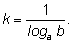
Коэффициент пропорциональности называют модулем перехода.
Отметим простые следствия выведенной формулы.
1)
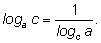
2)
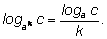
3)
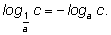
|
Упражнения
1. Докажите следующие формулы:
1)
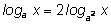
2)
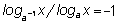
3)
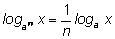
2. Дано число
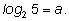 Выразите через а следующие числа:
Выразите через а следующие числа:
1)
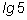
2)
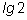
3)
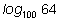
3. Вычислите:
1)
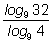
2)
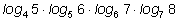
|
Упражнение.
Встроенный калькулятор (слева) умеет вычислять только натуральный
логарифм (логарифм по основанию e, где e = 2,718281828459... - иррациональное число, введённое
Эйлером, которое будет изучаться позже, ln (x) = logex ).
Используя калькулятор и ячейки для хранения
промежуточных результатов (перемещать в них числа из окна
калькулятора и обратно можно простым "перетягиванием мышкой " с
предварительным выделением числа той же мышкой).
1. Вычислите lg 2; lg 0,5; lg
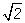
2. Вычислите log2 10;
log0,5 11;
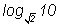
|
|
|
| |