|
Десятичные логарифмы
Среди различных оснований для вычисления логарифмов чаще всего
используется число
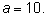 Логарифмы по такому основанию называются
десятичными и имеют специальное обозначение:
Логарифмы по такому основанию называются
десятичными и имеют специальное обозначение:
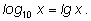
Особое положение десятичных логарифмов связано с использованием
десятичной системы счисления. Если мы запишем положительное число
x в стандартной форме, т. е. в виде
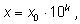 где
где
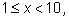 то получим, что
то получим, что
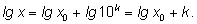 Но
Но 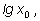 если
если
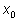 лежит в указанном интервале, является положительным числом, меньшим
1. Это означает, что мы представили
лежит в указанном интервале, является положительным числом, меньшим
1. Это означает, что мы представили
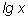 как сумму целого числа и положительной дроби, меньшей единицы, т. е.
k – это целая часть десятичного логарифма числа
x. По десятичной записи числа
x мы сразу можем приблизительно определить его
десятичный логарифм.
как сумму целого числа и положительной дроби, меньшей единицы, т. е.
k – это целая часть десятичного логарифма числа
x. По десятичной записи числа
x мы сразу можем приблизительно определить его
десятичный логарифм.
В частности, десятичный логарифм целого числа, записанного
k десятичными знаками, лежит в пределах от
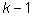 до
k.
до
k.
Натуральные логарифмы, число
e
Есть одно основание, которое в расчетах используется не реже, чем
число
10. Это знаменитое число
e, введенное Эйлером. Это число не является
рациональным, лежит между
2 и
3, и его первые десятичные знаки таковы:
e=2,718281828… .
|
Эйлер |
|
Леонард |
|

|
|
Годы жизни:
|
|
1707-1783 |
Логарифмы
по этому основанию называются натуральными и обозначаются с
помощью знака
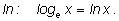
Чем же замечательно число
e ?
Подробнее мы узнаем об этом в главе, посвященной основам
математического анализа.
Сейчас лишь скажем следующее. С помощью степени с произвольным
действительным показателем мы определим показательную функцию
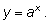 Показательная функция при
Показательная функция при
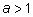 растет очень быстро, быстрее любой степени. Можно
определить скорость роста этой функции аналогично тому, как в физике,
исходя из функции, задающей положение
y точки в момент времени
x, определяют ее мгновенную скорость.
Оказывается, что показательная функция растет так быстро, что скорость
ее роста пропорциональна значению самой этой функции. Этот коэффициент
зависит от
а и участвует во многих расчетах. Число
e – это такое число, что скорость роста
показательной функции с основанием
e просто равна значению этой функции, т. е.
коэффициент пропорциональности, о котором шла речь выше, равен
единице, что, конечно, сильно облегчает расчеты.
растет очень быстро, быстрее любой степени. Можно
определить скорость роста этой функции аналогично тому, как в физике,
исходя из функции, задающей положение
y точки в момент времени
x, определяют ее мгновенную скорость.
Оказывается, что показательная функция растет так быстро, что скорость
ее роста пропорциональна значению самой этой функции. Этот коэффициент
зависит от
а и участвует во многих расчетах. Число
e – это такое число, что скорость роста
показательной функции с основанием
e просто равна значению этой функции, т. е.
коэффициент пропорциональности, о котором шла речь выше, равен
единице, что, конечно, сильно облегчает расчеты.
Связь между десятичными и натуральными логарифмами осуществляется с
помощью модуля перехода
k:
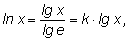 где
где
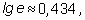 а
а
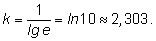
|
Порядки k знаменитых констант
|
Масса покоя электрона (в кг) |
9,11 × 10–31 |
k = –31 |
|
Электрический заряд (в А × с) |
1,60 × 10–19 |
k = –19 |
|
Скорость света (в м/с) |
2,99 × 108 |
k = 8 |
|
Диаметр Солнца (в м) |
1,39 × 109 |
k = 9 |
|
Диаметр нашей Галактики (в м): |
7,7 × 1019 |
k = 19 |
|
Масса Земли (в кг) |
5,98 × 1024 |
k = 24 |
Приближенные формулы для числа e
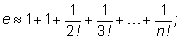
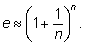
|