|
Сформулируем несколько простых и очевидных правил
комбинаторики.
Правило сложения
Пусть в множестве
А имеется
m элементов,
а в множестве
В –
n элементов.
Если у множеств
А и
В нет
общих элементов, то в их объединении число элементов равно
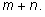
Можно сказать так, что если в двух мешках лежат разные предметы, и мы
ссыпаем их вместе, то, чтобы найти их общее количество, надо сложить
количества предметов в каждом из мешков.
Если для конечного множества
Х мы
через
|Х| обозначим
количество его элементов, то правило сложения можно записать так: |
Если
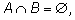то 
|
|
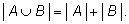
Это правило несложно обобщается на случай, когда у
множеств
А и
В есть
общая часть.
Правило умножения
Число пар, составленных из элементов множеств
А и
В, равно
произведению количеств элементов этих множеств.
Множество пар элементов двух множеств часто обозначают с помощью знака
произведения. Тогда правило умножения можно записать так: |
|
|
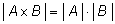
Правило умножения легко пояснить с помощью таблицы.
Если мы составим прямоугольную таблицу и занумеруем (обозначим) ее
строчки элементами множества
А, а
столбцы – элементами множества
В, то
клетки таблицы будут соответствовать парам
где
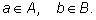Число клеток таблицы очевидно равно произведению числа строк и числа
столбцов. |
|
Примеры.
1. Рассмотрим произведение
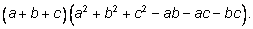Сколько одночленов (до приведения подобных) получится при
умножении «скобки на скобку»?
Этот же вопрос можно переформулировать так: сколько пар можно
составить из одночленов первой и второй скобок? В первой скобке
выберем любой из трех одночленов, во второй – любой из шести. Число
пар равно
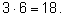
В этом примере используется правило умножения. |
| |
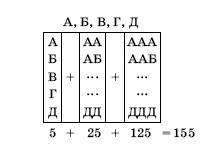 2)
Алфавит состоит из пяти букв. Сколько можно составить слов из букв
этого алфавита, имеющих не более трех букв?
Однобуквенных слов будет
5, двухбуквенных
–
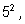трехбуквенных –
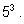Так как эти множества попарно не
пересекаются, то общее число слов (по правилу сложения) равно
 |
| |
|
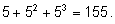 3)
В меню столовой указано
5 закусок,
3 первых
блюда,
4 вторых
и
3 десерта.
Каким числом способов можно заказать обед из четырех блюд?
При составлении заказа мы составляем четверки названий:
1) закуска;
2) первое блюдо;
3) второе блюдо;
4) десерт.
В первую строчку этой четверки мы вписываем любой из пяти данных
вариантов, во вторую – любой из трех и т. д. Общее число вариантов
будет равно произведению
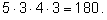
Это пример на обобщение правила умножения. Мы составляем не только
пары, но наборы из двух, трех, четырех и т. д. объектов. |
| |
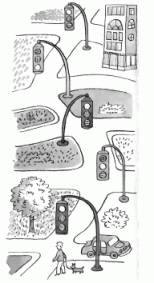 4)
На пяти перекрестках независимо друг от друга зажигают трехсекционные
светофоры. Каким числом способов это можно сделать?
Будем подряд зажигать светофоры. Первый можно зажечь тремя способами.
Зажигая второй, мы увеличим число вариантов втрое (получим пары
зажженных огней). При очередном включении мы также увеличиваем второе
число вариантов. В итоге получим число
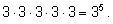
Можно сказать, что мы применили правило произведения, но составляли
наборы по
5 объектов
не из разных множеств, как в предыдущем примере, а из одного и того же
множества из трех возможных цветов.
Можно сказать иначе – у нас есть пять мест (светофоры), и мы должны
разместить на них три объекта (цвета) независимо друг от друга (с
повторениями).
|
| |