|
Пусть у множеств А и В общая часть насчитывает k
элементов. Тогда всего, в объединении множеств А и В, число элементов
равно
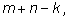т. е.
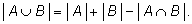
Понятно, что, складывая числа
m и
n, мы засчитываем общие элементы дважды.
Правило включения – исключения распространяют на объединение
произвольного числа множеств. Для трех множеств соответствующая
формула написана ниже. |
Теорема.
 |
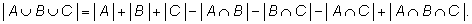
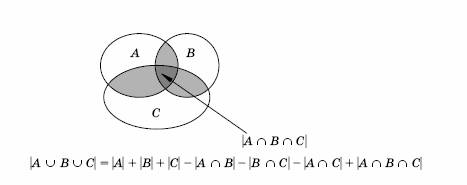Доказательство.
Для доказательства обозначим число элементов в каждой из
7 частей трёх множеств, находящихся в «общем
положении», некоторой переменной, а затем выразим через эти переменные
каждое слагаемое в левой и правой части. Подставив полученные
выражения в утверждение теоремы, убедимся в его правильности.
Другой способ рассуждений – убедиться в том, что элементы каждой из
указанных
7 частей множества подсчитаны в правой части,
причём, ровно по одному разу. Рассмотрим, например, элементы
пересечения
A и
B, не входящие в
C. В правой части они учитываются трижды: два
раза в слагаемых
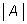и
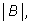один раз в слагаемом
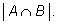Однако последнее в формулу входит со знаком минус, поэтому в
результате элементы указанной части учитываются ровно по одному разу.
|
|
Пример.
В классе
30 человек, каждый из которых изучает иностранный
язык.
20 человек изучает английский,
15 – французский и
17 – немецкий. При
 этом
в группах изучающих по два языка насчитывается по
10 человек. Сколько человек изучает все три языка?
Применяем формулу включения – исключения:
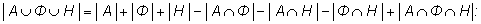
30 = 20 + 15 +17 - 10 - 10 - 10 + x ,
откуда x
= 8.
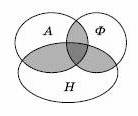
Буквами
А,
Ф и
Н обозначены множества учащихся, изучающих данный
язык. |
| |
|
|
| Упражнение.
Используя динамическую иллюстрацию, выполните следующие задания.
1. Решите задачу: "Имеется некоторое
множество из 100 различных натуральных чисел. В нём 50 чётных чисел,
40 чисел, кратных (делящихся нацело) трём, 35 чисел, кратных пяти,
15 чисел, кратных шести, 10 чисел, заканчивающихся нулём, 8 чисел,
кратных 15 и 3 числа, кратные 30". Есть ли в этом множестве, числа
не делящиеся ни на 2, ни на 3, ни на 5? сколько? Есть ли нечётные
числа, кратные трём? Сколько? Есть ли числа, заканчивающиеся на 5?
Сколько?
2. Проиллюстрируйте решение задачи из
приведённого выше примера. Для этого попробуйте подобрать такое
значение количества человек, изучающих все три языка (пересечение
всех трёх множеств), чтобы число людей не изучающих языки (которое
вычисляется в динамической иллюстрации стало равным нулю).
3. Попробуйте проиллюстрировать решение
задачи из следующего - "странного" - примера. Почему динамический
иллюстратор выдаёт ошибку. Объясните.
4*. Попробуйте ввести более ли, менее ли
случайные числа в динамический иллюстратор. Если данные не подходят,
попробуйте менять их по одному, пока не подберёте комбинацию, дающую
решение. Напишите условия, которым должны удовлетворять исходные
данные задачи, чтобы задача имела решение. |
| |
"Странный" пример.
В классе
30 человек, каждый из которых изучает иностранный
язык.
20 человек изучает английский,
15 – французский и
10 – немецкий. При
этом
в группах изучающих по два языка насчитывается по
8 человек. Сколько человек изучает все три языка?
Применяем формулу включения – исключения:
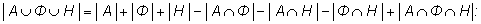
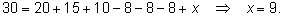
Буквами
А,
Ф и
Н обозначены множества учащихся, изучающих данный
язык. |
| |