Самая древняя игральная кость, т. е. кубик с нанесенными на грани
шестью различными знаками, была найдена при раскопках в северном
Ираке. Ее возраст составил около 5 тысяч лет. Комбинации, возникающие
при бросании игральной кости и других играх, всегда привлекали людей,
никак не связанных с математикой, потому что наименование нашего вида,
homo sapiens (человек мыслящий), уже давно (по мере разочарования в
мыслительных способностях человека) стало ставиться рядом с
наименованиями homo faber (человек делающий) и homo ludens (человек
играющий).
| Паскаль |
| Блез |
|
Годы жизни: |
| 1623-1662 |
Различные игры – кости, карты, лото, домино и пр. и
пр. – ставят перед человеком вопросы, требующие тщательного анализа и
применения серьезной математической техники. Постепенно выяснилось,
что аналогичные вопросы возникают не только в играх, но и в самых
разнообразных и внешне далеких друг от друга сферах человеческой
деятельности – экономике и планировании, лингвистике и криптографии,
теории стрельбы и организации транспорта. С помощью комбинаторики и
тесно связанных с ней таких разделов математики как статистика и
теория вероятностей, удалось нащупать строгие закономерности там, где
их не должно было бы быть по самому смыслу – в мире случайных явлений,
среди хаоса и беспорядка.
Среди родоначальников комбинаторики и теории
вероятности надо назвать знакомые имена – Паскаля и Ферма, Бернулли и
Лапласа и, разумеется, Эйлера.
Легенда сообщает, что 29 июля 1654 года Паскаль написал письмо Ферма,
в котором рассказал о «скандале в доме математики», обнаруженном
французским аристократом, страстным игроком и достаточно образованным
человеком, носившим имя де Мере. Вопрос состоял в следующем. Сколько
раз надо подряд бросить игральную кость, чтобы шансы того, что хоть
раз выпадет шестерка, превысили половину? На этот легкий вопрос де
Мере знал правильный ответ – четыре. (Как само собой разумеющееся,
Паскаль в письме Ферма называет количество комбинаций – при четырех
бросаниях кости в 625 случаях ни разу не выпадет шестерка и в 671 случае она выпадет хотя бы один раз.) Более
распространенной была игра с одновременным бросанием пары костей. Как
нечто очевидное, де Мере считал, что отношение 4:6
(числа необходимых бросаний к числу возможных исходов) сохранится и
при бросании пары костей. Общее число исходов в этом случае равно
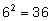и, следовательно, нужно произвести 24 бросания пары костей ( 24:36=4:6 ), чтобы шансы на выпадение двух шестерок превысили
половину. Однако его опыт игрока говорил и о том, что это не так и
необходимо не 24, а 25 бросаний. |
| Ферма |
| Пьер |
|
Годы жизни: |
| 1601-1665 |
| Бернулли |
| Якоб |
|
Годы жизни: |
| 1654-1705 |
Эта задача де Мере (а он является автором еще
нескольких важных и более трудных вопросов) будет нам вполне по
силам.
Общее число комбинаций сейчас уже велико, но точные вычисления Паскаля
показали, что доля успешных вариантов при 24 бросаниях равна приблизительно 0,4914 и лишь при 25 бросаниях чуть превосходит половину – 0,5055. Надо было долго играть в кости, чтобы
почувствовать разницу между этими двумя дробями.
Несмотря на то, что комбинаторика является столь древним разделом
математики, в школе ее изучали мало. Произошедший в последние
десятилетия взрыв интереса к комбинаторике во многом объясняется
наступлением компьютерной эры и повышением роли так называемой
дискретной математики, имеющей дело прежде всего с конечными
множествами. Нашей задачей является ознакомление с методами
комбинаторики, которые позволят выработать общие принципы решения
различных интересных задач и подготовиться к восприятию идей теории
вероятности.
Комбинаторика родилась как «наука о забавных и приятных задачах,
которые решаются в числах». Так была названа замечательная книга, не
потерявшая своего значения до сих пор и написанная в 1612 году
французским математиком, философом и поэтом Баше де Меризиаком. К
забавности и приятности предмета постепенно присоединилась глубина и
польза. В философско-математическом плане на смену жестко
детерминированным (определенным и незыблемым) представлениям об
устройстве мира пришло убеждение в его неопределенности и
случайности. Перебор случаев (вариантов) – это уже комбинаторика.
| Лаплас |
| Пьер-Симон |
|
Годы жизни: |
| 1749-1827 |
Однако просто перечисление вариантов, даже если оно сопровождается
хорошим алгоритмом перебора (что удается не всегда), – это только
начало. Математика научилась оценивать «удельный вес» вариантов,
создав теорию вероятностей – самое значительное, но не единственное
продолжение комбинаторики. Комбинаторика является одним из оснований
всей дискретной математики, исследующей разные конструкции с участием
конечных множеств, основанием теории информации.
Конечно, не нужно думать, что непрерывная и дискретная математика
противоположны друг другу. Уже теория вероятностей в своем развитии
продемонстрировала слияние методов и идей комбинаторики и
математического анализа. Это слияние лежит и в основе информатики.
Может быть, поэтому известный американский ученый, ведущий специалист
в области информатики Д. Кнут написал очень содержательную и вполне
доступную школьникам книгу «Конкретная математика», в названии которой
соединяются слова КОНтинуальная (непрерывная) и дисКРЕТная математика.
|
