| Размещения |
|
Размещение – это поочередный выбор элементов из
данного множества. |
|
Обычно размещение рассматривают не как процесс, а
как его результат. Можно представить себе, что у нас есть пустые
клетки, места, на которые мы должны поместить элементы данного
множества. Типичным примером такой задачи является составление слов из
букв данного алфавита. Возьмем алфавит из пяти букв
a,
b,
c,
d,
e и будем составлять трехбуквенные слова. Под словом
понимается последовательность из нескольких букв данного алфавита (не
обязательно осмысленная).
Возможны два принципиально различных условия – буквы можно повторять
независимо друг от друга или все буквы должны быть различны. Ситуацию
можно описать так: в мешке лежат буквы и заготовлены места, куда мы
будем ставить вытащенные из мешка буквы. Условия различаются в
зависимости от того, поставив букву на одно место, т. е. вписав ее в
одну клетку, возвращаем ли мы букву в мешок, чтобы ее можно было
использовать в дальнейшем, или не возвращаем, и тогда все следующие
вытащенные из мешка буквы будут различными.
Итак, подсчитаем число трехбуквенных слов, составленных из
пятибуквенного алфавита.
Первый вариант: буквы могут повторяться.
На первое место (в первую клетку) мы поставим любую из
5 букв. На второе место также поставим любую из
пяти букв. Получим пары (двухбуквенные слова). По правилу умножения
число таких пар
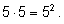 На третье место снова поставим любую букву, независимо от того, какие
буквы стоят на первых двух местах. Число слов увеличится в пять раз –
мы составляем «пару» из двухбуквенного слова (их было
На третье место снова поставим любую букву, независимо от того, какие
буквы стоят на первых двух местах. Число слов увеличится в пять раз –
мы составляем «пару» из двухбуквенного слова (их было
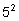 ) и еще одной буквы. Получим
) и еще одной буквы. Получим
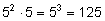 вариантов.
вариантов.
Процесс составления размещений с повторениями удобно представить в
виде схемы, называемой деревом.
Второй вариант: буквы должны быть различны.
Снова на первое место поставим любую из пяти букв. На второе место
можно поставить любую из четырех оставшихся букв. Число пар
(двухбуквенных слов с неповторяющимися буквами) будет равно
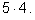 Дописывая третью букву, мы будем иметь лишь три возможности, т. е.
число вариантов умножится на
3. Получим
Дописывая третью букву, мы будем иметь лишь три возможности, т. е.
число вариантов умножится на
3. Получим
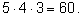
Сформулируем результат в общем виде. |
|
Пусть у нас есть множество, содержащее
n элементов, которые мы хотим разместить на
k местах.
1) Число размещений
n элементов на
k местах с повторениями равно
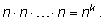
2) Число размещений
n элементов на
k местах без повторений равно
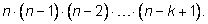 |
|
Заметим, что в каждой формуле
k множителей. В первом случае все множители
одинаковы и произведение
k множителей есть
k-ая степень числа
n. Во втором случае каждый множитель на единицу
меньше предыдущего. Первый из них равен
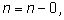 поэтому
k-ый по номеру равен
поэтому
k-ый по номеру равен
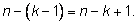
Иногда число размещений
n элементов на
k местах без повторений обозначают через
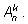 Получим формулу
Получим формулу
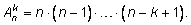
Перестановки |
|
Перестановка – это расположение объектов в
определенном порядке. |
|
Обычно перестановку рассматривают как упорядоченный
набор, составленный из всех элементов множества. Можно представить
себе, что у нас есть множество, содержащее
n элементов, которые мы должны расположить (без
повторений) на
n местах. В такой формулировке мы приходим к
задаче о числе размещений
n объектов со следующими двумя условиями: число
мест равно числу объектов и объекты не должны повторяться.
Ответ на такую задачу нам известен: надо взять произведение целых
чисел, начиная с
n и так, чтобы каждое следующее было на единицу
меньше предыдущего. Так как число множителей равно
n, то последний из них будет равен единице.
Получим правило.
Число перестановок
n элементов равно произведению всех целых чисел
от
1 до
n.
Произведение
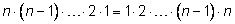 обозначается
обозначается
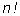 (
n факториал).
(
n факториал).
Составим таблицу факториалов.
1! = 1
2! = 2
3! = 6
4! = 24
5! = 120
6! = 720
7! = 5 040
8! = 40 320
9! = 362 880
10! = 3 628 800
Видно, что факториалы с ростом
n растут очень быстро. Поэтому перебирать все
перестановки
n элементов невозможно даже при сравнительно
небольших значениях
n. Например, число
100! имеет порядок
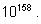
 Число Число
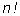 получается из числа
получается из числа
 умножением на
n, т. е.
умножением на
n, т. е.
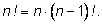 Если число перестановок из
n элементов обозначить через
Pn, то мы получаем
рекуррентную формулу:
Если число перестановок из
n элементов обозначить через
Pn, то мы получаем
рекуррентную формулу:
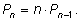
На рисунке изображено дерево для составления перестановок при
n = 2, 3, 4, иллюстрирующее эту формулу.
|
| |