Сочетание – это одновременный выбор нескольких
элементов из данного множества. |
Сочетание обычно рассматривают как результат такого
выбора, тогда это будет неупорядоченный набор элементов, взятых из
заданного конечного множества. Можно представить себе, что у нас есть
множество из n элементов и мы хотим выбрать k из них (без учета порядка, в котором мы их
выбираем). Обозначим число таких выборок (сочетаний из n элементов по k ) через
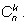
Чтобы найти число
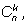обратимся к задаче подсчета числа размещений без повторений.
Предположим, что мы хотим разместить на k местах различные элементы из множества в n элементов. Сначала выберем те k из них, которые займут эти места. По
определению число этих выборок равно
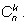Далее, взяв любую из этих выборок (в ней k различных элементов), переставим все ее
элементы. Это можно сделать
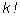способами. Ясно, что перестановки, полученные из
разных выборок, будут различными, а с другой стороны таким способом мы
получим все размещения без повторений, число которых
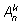нам известно. По правилу умножения получим формулу
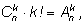откуда найдем число
|
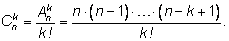
Число сочетаний из n элементов по k вычисляется по формуле
|
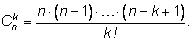
Легко заметить общие правила:
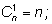
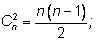
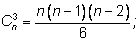
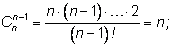
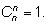
Добавим к этому формулу
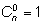(считая, что выбрать 0 объектов можно одним способом – ничего не
взять).
Число
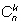можно записать по-другому:
В преобразованиях мы умножили числитель и знаменатель дроби на
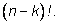В числителе мы получили
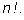
Итак, |
|
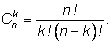
Чтобы сохранить эту формулу для
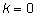и
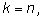будем считать, что
|
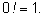
Вычисление числа
сочетаний через факториал приводит к дроби, числитель и знаменатель
которой очень велики, но после сокращения они существенно
уменьшаются. Есть другой путь вычисления сочетаний, основанный на
формуле
.
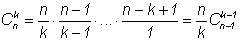Алгоритм вычисления числа сочетаний
:
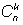Шаг 1. В качестве начального значения
результата взять 1, а в качестве первого множителя -
дробь
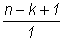
Шаг 2. Умножить результат на текущий множитель -
дробь, после чего числитель и знаменатель дроби увеличить на 1.
Шаг 3. Повторять шаг 2 до тех пор, пока дробь не станет
равной
.
|
|
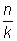Упражнение. Используя встроенный инструмент,
вычислите по алгоритму следующие числа сочетаний:
,
.
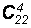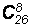Полученный результат (второе число
сочетаний) показывает число различных паролей, которые можно составить из 8 строчных букв латинского алфавита.
Какое число паролей той же длины можно составить из 33 букв русского алфавита?
Как изменится первый ответ, если кроме строчных использовать и заглавные
буквы латинского алфавита? |
| |
| Задание. Докажите, что в процессе выполнения алгоритма всегда
будут получаться целые числа. |
| |