|
Числа
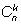 обладают многими интересными свойствами. Перечислим
наиболее известные из них.
обладают многими интересными свойствами. Перечислим
наиболее известные из них. |
|
1)
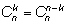
 Это
можно проверить с помощью формулы: Это
можно проверить с помощью формулы:
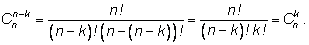
|
|
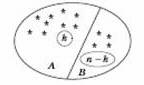
Но интереснее и полезнее можно доказать это
свойство, используя из определение числа сочетаний. Чтобы выбрать
k элементов из множества в
n элементов, можно указать те из них, которые
останутся, не будут выбраны. Если мы выбираем
k элементов, то остается
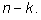 Поэтому число выборок по
k элементов (из
n ) равно числу выборок по
Поэтому число выборок по
k элементов (из
n ) равно числу выборок по
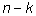 элементов.
элементов.
|
|
2)
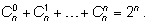
|
|
Подсчитаем двумя способами общее возможное число
выборок из множества, содержащего
n элементов (число всех подмножеств
n -элементного множества).
С одной стороны это число равно
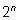 – для каждого элемента есть две возможности: попасть или не попасть в
выбираемое подмножество, причем для каждого элемента эти возможности
выбираются независимо друг от друга.
– для каждого элемента есть две возможности: попасть или не попасть в
выбираемое подмножество, причем для каждого элемента эти возможности
выбираются независимо друг от друга.
Это же число можно получить иначе – сначала зафиксировать число
k элементов в подмножестве. Получим число
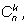 а затем сложим по всем
k, чтобы найти общее число вариантов.
а затем сложим по всем
k, чтобы найти общее число вариантов.
|
3)
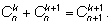 – рекуррентное соотношение, связывающее числа
сочетаний.
– рекуррентное соотношение, связывающее числа
сочетаний.
|
|
Представим себе, что к
n элементам данного множества мы добавили еще
один, и из полученного множества хотим выбрать подмножество из
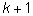 элемента. По определению это число равно
элемента. По определению это число равно
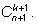 Все эти выборки мы разобьем на два сорта – те, которые содержат один
добавленный элемент, и те, которые его не содержат. Первых будет
Все эти выборки мы разобьем на два сорта – те, которые содержат один
добавленный элемент, и те, которые его не содержат. Первых будет
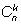 штук (один элемент уже взят, а из остальных надо взять
еще
k ), а вторых –
штук (один элемент уже взят, а из остальных надо взять
еще
k ), а вторых –
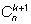 (все
(все
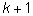 элементов берутся из исходного множества). Тем самым
элементов берутся из исходного множества). Тем самым
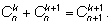
Это равенство лежит в основе построения так называемого треугольника
Паскаля, позволяющего быстро вычислять числа сочетаний
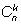 для небольших значений
n.
для небольших значений
n.
|
|
Треугольник Паскаля – это треугольник из целых
чисел, по боковым сторонам которого стоят единицы, а каждое число
внутри треугольника равно сумме двух чисел, стоящих над ним. |
|
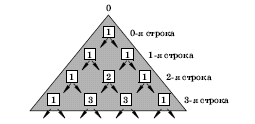 Легко
заметить, что в n-ой строке треугольника Паскаля на k–ом месте (места
нумеруем с нуля) стоит число Легко
заметить, что в n-ой строке треугольника Паскаля на k–ом месте (места
нумеруем с нуля) стоит число
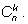
Действительно, на сторонах треугольника стоят единицы, так как
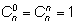 (добавим еще
(добавим еще
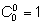 ), а над элементом
), а над элементом
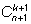 стоят элементы
стоят элементы
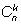 и
и
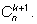 Так как
Так как
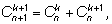 то мы видим, что закон образования элементов треугольника из чисел
сочетаний совпадает с законом образования элементов треугольника
Паскаля.
то мы видим, что закон образования элементов треугольника из чисел
сочетаний совпадает с законом образования элементов треугольника
Паскаля.
Полезно заметить, что в треугольнике Паскаля самый большой элемент
строки стоит в ее середине (он один при четном
n и их два одинаковых при нечетном
n ).
При этом члены строки возрастают к ее середине, а потом убывают.
Рассматривая треугольник Паскаля, можно обнаружить много новых свойств
сочетаний.
|
4)
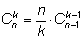 – еще одно рекуррентное соотношение.
– еще одно рекуррентное соотношение.
|
|
Решим двумя способами следующую задачу: из группы в
n человек надо выбрать команду в
k человек и среди них назначить одного капитана
команды.
Сначала можно выбрать всю команду (число способов –
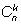 ) и из нее выбрать капитана (
k способов). Всего получится
) и из нее выбрать капитана (
k способов). Всего получится
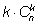 способов.
способов.
Можно сначала из всей группы выбрать капитана (
n способов), а затем из оставшихся выбрать
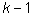 рядовых членов команды (
рядовых членов команды (
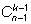 ) – всего
) – всего
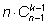 способов.
способов.
Результат:
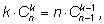 т. е.
т. е.
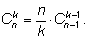
|
| |