Задача 1. Доска Гальтона и равенство  
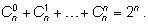
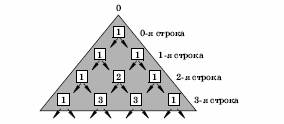
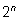Представим себе частицу, которая на каждом шаге (например, через  1  секунду) распадается на  2,  и эти половинки попадают в две заготовленные корзины. Число корзин на каждом шаге увеличивается на  1.  Получим схему, изображенную на рисунке. На  n-ом шаге во всех корзинах вместе будет    частиц (на каждом шаге число частиц удваивалось), а число частиц в одной корзине равно сумме этих чисел в двух корзинах,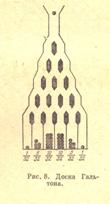 расположенных выше этажом. Поэтому число частиц в  k-ой корзине ( 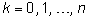) на  n-ом шаге равно  
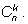
(Существует устройство – доска Гальтона, демонстрирующая эту идею. Ее изображение вынесено на обложку известной книги из библиотечки журнала «Квант»: А.Н. Колмогоров, И.Г. Журбенко, А.В. Прохоров. «Введение в теорию вероятностей».
Механические шарики один за другим попадают в самый верхний канал. Наткнувшись на первое острие, они должны выбрать путь направо или налево. Затем происходит второй выбор и т.д.)

Задача 2. Число анаграмм.
Как подсчитать число анаграмм для слова с повторяющимися буквами, например, для слова колокол. Общее число букв –  7,  из них  3  различных –  к  (повторяется  2  раза),  л  ( 2  раза) и  о  ( 3  раза).
Вычислим число анаграмм способом, аналогичным тому, которым мы находили формулу для числа 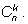   Пусть искомое число анаграмм равно  x.  Теперь сделаем одинаковые буквы разными (например, запишем их разными шрифтами). «Размножая» букву  к,  мы удвоим число анаграмм, затем, делая ту же операцию для буквы  л,  мы снова удвоим, а переставляя три по-разному записанные буквы  о,  мы увеличим число вариантов в 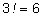   раз. В итоге получим все анаграммы слова из  7  различных букв. Итак, 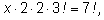   откуда  

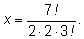
Проделывая то же рассуждение в общем виде, получим следующую полезную формулу. Пусть у нас есть  n  объектов  k  различных видов. Пусть первый вид повторяется 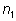   раз, второй – 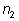   раз, …,  k-ый – 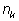   раз. (Разумеется, 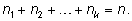  ) Число перестановок этих объектов равно  

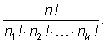
Применим эту формулу к следующей задаче.
Сколько есть семизначных чисел, имеющих в записи две двойки, три тройки и две пятерки?
Задача сводится к стандартной задаче об анаграммах с повторяющимися буквами . Ответ:  

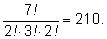
Задача 3. Распределение билетов.
В классе  20  человек. Мы хотим пятерым из них дать билеты в театр. Каким числом способов это можно сделать?
Сначала выберем тех пятерых, которые пойдут в театр. Пусть это можно сделать  x  способами. Затем рассадим эту пятерку на места (раздадим билеты). Это можно сделать 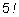   способами (пример  6 ). Общее число вариантов получим по правилу произведения: 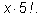 . Сравнивая два ответа 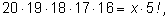   найдем  x :  
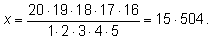
Мы нашли число сочетаний (выборок, подмножеств) из  20  элементов по  5 :  
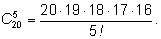
Приведем пример на использование различных правил комбинаторики.

Задача 4. Секретный код.
Секретный код составляется из двух букв и трех цифр. При этом буквы выбираются из  5  различных и могут повторяться, а цифры – из  10  возможных и должны быть различными. Сколькими способами мы можем составить  3  различных кода?
Общее число кодов: 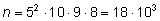   – мы на двух первых местах размещаем буквы (независимо друг от друга), а на следующих трех местах – цифры без повторений.
Из полученного множества кодов мы должны выбрать (одновременно) три. Это можно сделать 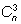   способами. При 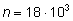   это число равно  

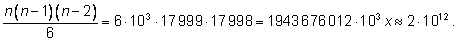
Задача 5. Задача о монетах и карманах.
Каким числом способов можно разложить  10  одинаковых монет в  3  различных кармана?
Задача совпадает с задачей представления числа  10  в виде упорядоченной суммы трех неотрицательных слагаемых. (Каждое слагаемое – число монет в соответствующем кармане.) Используем готовую формулу (пример  12 ). Ответ:  
 

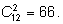
Задача 6. Число одночленов.
Сколько есть различных одночленов степени  n  с  k  буквами (коэффициент считаем равным  1 ).
Одночлен степени  n  с  k  буквами записывается в ви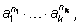де    где 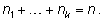   Он определяется упорядоченным представлением числа  n  в виде суммы  k  неотрицательных слагаемых. (Упорядоченное означает, что, например, представления 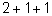   и 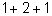   мы считаем различными.)
Итак, подсчитаем число упорядоченных представлений числа  n  в виде суммы  k  неотрицательных слагаемых.
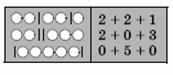
Изобразим число  n  в виде набора  n  одинаковых символов (кружков). Поставим между этими символами одну перегородку (палочку). Она определит разбиение числа  n  на сумму двух слагаемых. Чтобы получить  k  слагаемых, надо поставить 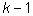   перегородку (рис. 3-15). Теперь мы должны переставить между собой n кружков и 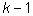   перегородку. Можно считать, что у нас есть 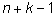   мест, и мы должны выбрать те  n  мест, где стоят кружки (или же 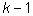   мест, где стоят перегородки). Это можно сделать 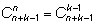   способами.
При 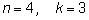   получаем число  

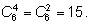
Задача 7. Схема блуждания по городу.
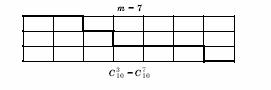Город разбит на блоки горизонтальными и вертикальными улицами.
Каким числом способов можно пройти кратчайшим путем из одного угла города в противоположный?
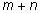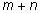Пусть число блоков в горизонтальном направлении равно  n,  а в вертикальном –  m  (число улиц в каждом направлении на  1  больше). Полный путь содержит    шагов (движение вдоль одного блока), из которых  m  должно быть сделано по вертикали, а  n  – по горизонтали. Общее число путей равно числу выборок из    шагов тех  m,  которые будут сделаны по вертикали (остальные – по горизонтали). Ответ:
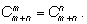