| Формула бинома Ньютона |
|
Бином Ньютона – это формула разложения степени
двучлена (бинома)
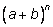 в виде многочлена от
a и
b. в виде многочлена от
a и
b. |
|
Запишем разложения бинома Ньютона для нескольких
первых значений
n.
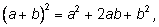
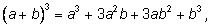
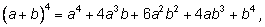
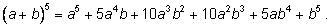
Чтобы найти коэффициент при
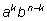 в разложении бинома
в разложении бинома
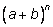 в
общем случае, представим себе, что мы перемножаем
n скобок (каждый
член на каждый) и приводим подобные члены. Член в
общем случае, представим себе, что мы перемножаем
n скобок (каждый
член на каждый) и приводим подобные члены. Член
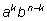 встретится
столько раз, сколько можно указать
k скобок (из
n возможных), из которых мы возьмем множитель
а (а из остальных автоматически возьмем
b ). Это число равно числу выборок
k скобок из
n возможных, которое носит название числа
сочетаний из
n по
k и обозначается встретится
столько раз, сколько можно указать
k скобок (из
n возможных), из которых мы возьмем множитель
а (а из остальных автоматически возьмем
b ). Это число равно числу выборок
k скобок из
n возможных, которое носит название числа
сочетаний из
n по
k и обозначается
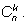
В этих обозначениях формула имеет следующий вид:
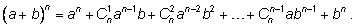
Иными словами, число сочетаний из
n по
k равно коэффициенту при члене
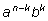 в разложении
n-ой степени двучлена в разложении
n-ой степени двучлена
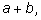 поэтому числа
сочетаний называют иначе биномиальными коэффициентами. поэтому числа
сочетаний называют иначе биномиальными коэффициентами.
Эту связь можно использовать для вывода свойств сочетаний
алгебраическими методами. Такой подход к выводу свойств комбинаторных
объектов носит название метода производящих функций.
|
|
Динамические примеры.
|
Упражнения. Используя встроенные инструменты
выполните следующие упражнения.
1. Просмотрите коэффициенты бинома
9-ой
степени, для этого в
качестве коэффициентов введите единички (в выражение бинома
для суммы
x и
y),
а затем меняйте показатели
степени при
x от
0 до
9.
2. Посмотрите как меняются величины
коэффициентов и их знаки на примере бинома
7-ой степени
для разности
x и
y.
3. Верно ли, что все
коэффициенты бинома
n-ой степени делятся на
n. Проверьте гипотезу на двух предыдущих
примерах, далее для значений
n от
10 до
17. Сформулируйте гипотезу о делимости.
Попробуйте обосновать гипотезу теоретически.Указание.
Для работы с инструментом надо
ввести степень многочлена (бинома) и коэффициенты
при
x и
y, а затем указать степень
x в искомом члене разложения. Степень
y этого члена будет вычислена автоматически,
а справа от выражения бинома появится соответствующий
одночлен. |
Замечание
При разложении многочлена (полинома)
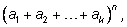 чтобы,
вычислить коэффициент при чтобы,
вычислить коэффициент при
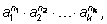 мы выбираем скобки с указанными
повторениями, т.е из мы выбираем скобки с указанными
повторениями, т.е из
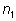 скобок мы берем множитель
скобок мы берем множитель
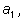 из из
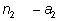 и т.д. Он равен
и т.д. Он равен
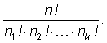
Эти коэффициенты называют полиномиальными коэффициентами. |
Например, возведем трехчлен
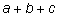 в четвертую степень. в четвертую степень.
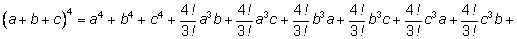
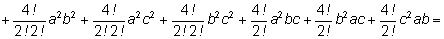
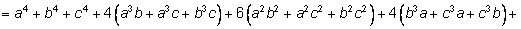
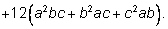
При
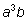 коэффициент равен коэффициент равен
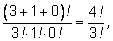 при при
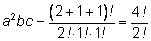 и т. д.
и т. д.
|
Свойства биномиальных коэффициентов
Биномиальные коэффициенты обладают большим количеством свойств.
Выпишем основные из них.
|
Свойство 1.
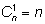 |
|
Для доказательства обратимся к основному
рассуждению о раскрытии скобок: число
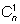 равно числу способов выбрать
одну скобку из
n, которое очевидно равно
n.
равно числу способов выбрать
одну скобку из
n, которое очевидно равно
n.
|
Свойство 2.
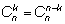 – биномиальные коэффициенты, равноотстоящие от концов,
равны между собой.
– биномиальные коэффициенты, равноотстоящие от концов,
равны между собой. |
|
Для доказательства достаточно поменять в формуле
a и
b местами. Левая часть при этом не изменится, а в
правой коэффициент при
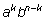 станет коэффициентом при
станет коэффициентом при
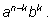
|
Свойство 3.
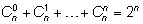 – сумма биномиальных коэффициентов при фиксированном
n равна
– сумма биномиальных коэффициентов при фиксированном
n равна
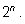 |
Для доказательства подставим вместо
a и
b единички.
Сразу получим искомое тождество.
|
Свойство 4.
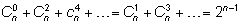 – суммы биномиальных коэффициентов, стоящих на четных и
на нечетных местах, равны между собой (и равны по половине от общей
суммы).
– суммы биномиальных коэффициентов, стоящих на четных и
на нечетных местах, равны между собой (и равны по половине от общей
суммы). |
|
Для доказательства подставим сначала
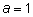 и
и
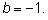 Перенеся вправо все члены с отрицательным знаком, получим первое из
равенств. Чтобы доказать второе, воспользуемся свойством
3. Обе суммы одинаковы, а их сумма равна
Перенеся вправо все члены с отрицательным знаком, получим первое из
равенств. Чтобы доказать второе, воспользуемся свойством
3. Обе суммы одинаковы, а их сумма равна
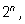 следовательно, каждая из сумм равна
следовательно, каждая из сумм равна
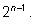
|
|
Свойство 5.
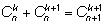 – рекуррентное соотношение, связывающее биномиальные
коэффициенты для соседних степеней.
– рекуррентное соотношение, связывающее биномиальные
коэффициенты для соседних степеней. |
|
Для доказательства рассмотрим равенство
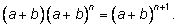
Найдем коэффициент при
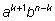 в обеих частях равенства. Слева он получится при
приведении двух подобных членов:
в обеих частях равенства. Слева он получится при
приведении двух подобных членов:
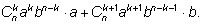 Справа ему будет соответствовать коэффициент
Справа ему будет соответствовать коэффициент
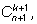 что и доказывает формулу.
что и доказывает формулу.
Примеры использования бинома Ньютона |
Пример 1. Разложить бином
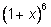 по степеням
x. по степеням
x.
Применяем формулу бинома Ньютона:
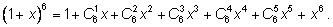
Значения биномиальных коэффициентов находим последовательно по формуле
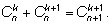 Например, Например,
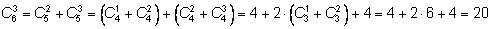
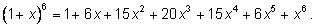
|
| |
Пример 2. Доказать формулу
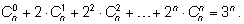
Подставляем в формулу для разложения
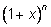 значение значение
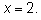 Получаем
требуемый результат. Получаем
требуемый результат. |
| |
Пример 3. Доказать соотношение
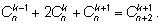
Используем рекуррентное соотношение
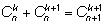
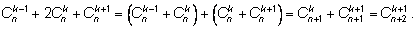
|
| |