|
Тригонометрия возникла и развивалась как часть астрономии. Вся история
человечества сопровождалась наблюдениями за движением небесных тел,
поэтому историю тригонометрии невозможно проследить до ее истоков. Как
с имени Евклида можно начать отсчет развития геометрии, так с имени
Птолемея (100-170) разумно связать исходную точку в описании
астрономии и тригонометрии. |
|
 Птолемей
(около 100 – 170) Птолемей
(около 100 – 170)
Древнегреческий математик и астроном. Работал в Александрии.
Прославился «Альмагестом» – «великим математическим построением
астрономии» трудом в 13 книгах, в которых описал стройную
геоцентрическую теорию строения Вселенной. Доказал теорему о вписанном
четырехугольнике (теорема Птолемея), изложил сведения о сферической и
прямолинейной геометрии, построил точные тригонометрические таблицы.
Первым усомнился в очевидности евклидовского постулата о параллельных
и пытался доказать его.
|
|
Клавдий Птолемей был одним из последних в ряду
блестящих древнегреческих мыслителей. Его описание Солнечной системы в
течение четырнадцати веков, вплоть до открытий Коперника, была
общепринятой системой устройства Вселенной. Как «Начала» Евклида
заключали в себе свод математических знаний, приобретенных
человечеством, так и «Альмагест» Птолемея представлял собой исходную
энциклопедию астрономии.
Астрономические таблицы Птолемея, сохранившиеся до нашего времени,
равнозначны тригонометрическим таблицам, позволяющим вычислять синусы
с шагом
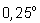 с пятью верными десятичными знаками. Для построения таблиц Птолемею
пришлось не только применить построенную к его времени евклидову
геометрию, но и доказать много новых фактов.
с пятью верными десятичными знаками. Для построения таблиц Птолемею
пришлось не только применить построенную к его времени евклидову
геометрию, но и доказать много новых фактов.
Если мы с именем Декарта связываем включение геометрии евклидовых
«Начал» в общий контекст математики, то аналогичную роль для
тригонометрии птолемеева «Альмагеста» сыграл немецкий математик и
астроном И. Мюллер (1436-1476), более известный под именем
Региомонтана. Его труд «О треугольниках всех видов» содержал таблицы
синусов через
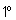 с точностью до
7 знаков.
с точностью до
7 знаков.
Так же, как корни, степени и логарифмы, до тех пор, пока они служат
для формул, преобразований и вычислений, мы относим к алгебре, так и
синусы – косинусы со всем калейдоскопом тригонометрических формул
можно отнести к этому разделу математики. Новый этап в развитии и
применении всех этих понятий наступает тогда, когда мы изучаем
изменение их значений при изменении аргумента (числа или угла). Зная,
как вычисляются синус, косинус, тангенс, котангенс для произвольного
числа, мы построим соответствующие функции и будем изучать их свойства
по общим правилам исследования функций. Так же и в истории
тригонометрии на смену алгебре тригонометрических формул и
преобразований пришел математический анализ тригонометрических
функций. Начиная с основополагающих работ Ньютона, Лейбница и И.
Бернулли, выполненных к началу XVIII века, роль тригонометрии в общей
теории функции была прояснена в начале XIX века французским
математиком Ж. Фурье, теория которого лежит в основе принципов
передачи сигналов (звука, изображения и т. п.) вплоть до наших дней.
Современный вид учение о тригонометрических функциях приняло в работах
Леонарда Эйлера.
|
|
 Леонард
Эйлер (1707-1783) Леонард
Эйлер (1707-1783)
Родился в Швейцарии, но большую часть жизни прожил и проработал в
России, женился на русской, опубликовал в России большинство своих
трудов, умер и похоронен в Петербурге.
Классический труд Эйлера «Введение в анализ бесконечных» переиздается
до сих пор. Именем Эйлера названы десятки теорем, формул и понятий из
всех областей математики. Мы столкнемся с именем Эйлера повсюду – в
геометрии (прямые Эйлера в треугольнике, формула Эйлера
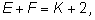 связывающая число вершин, граней и ребер многогранника), теории чисел
(функция Эйлера
связывающая число вершин, граней и ребер многогранника), теории чисел
(функция Эйлера
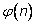 – количество на-туральных чисел до
n, взаимно простых с
n ), теории графов (эйлеровы пути – конфигурации, которые
можно начертить, не проходя дважды по одному участку), математическом
анализе (впечатляющая формула Эйлера
– количество на-туральных чисел до
n, взаимно простых с
n ), теории графов (эйлеровы пути – конфигурации, которые
можно начертить, не проходя дважды по одному участку), математическом
анализе (впечатляющая формула Эйлера
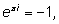 связывающая знаменитые числа), тригонометрии (ему принадлежит
большинство современных обозначений в теории тригонометрических
функций), комбинаторике (задача Эйлера о
36 офицерах) и т.д.
связывающая знаменитые числа), тригонометрии (ему принадлежит
большинство современных обозначений в теории тригонометрических
функций), комбинаторике (задача Эйлера о
36 офицерах) и т.д.
|
| |