|
Из формул двойных углов
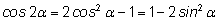 можно получить формулы для синуса и косинуса половинного угла.
можно получить формулы для синуса и косинуса половинного угла.
Сначала
запишем:
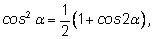
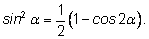
Затем в этих формулах подставим
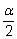 вместо
вместо
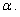
Получим:
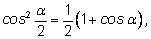
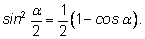
Извлекая корень, получим:
|
|
|
|
Для того, чтобы раскрыть модули, надо знать, в
какой четверти лежит угол
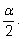
Обилие тригонометрических формул связано с тем, что
между основными тригонометрическими функциями – синусом, косинусом,
тангенсом и котангенсом – есть соотношения, которые позволяют
по-разному написать одно и то же выражение. Возникает вопрос: нельзя
ли выбрать одну какую-нибудь функцию и через нее выражать все
остальные?
Если в качестве такой функции мы выберем синус, то во
многих формулах появятся квадратные корни.
Так, например, выражая
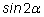 через
через
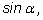 мы получим
мы получим
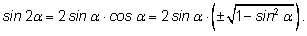
Такие формулы неудобны.
Оказывается, что все тригонометрические функции от аргумента
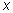 (и от
(и от
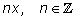 ) выражаются через тангенс угла
) выражаются через тангенс угла
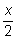 рационально, т.е. без квадратных корней.
рационально, т.е. без квадратных корней.
Выведем эти полезные функции.
Напишем формулы двойного угла для исходного угла
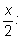
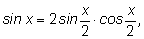
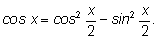
Представим число
1 в виде
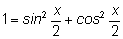 и поделим на это выражение правые части последних формул:
и поделим на это выражение правые части последних формул:
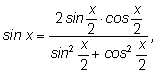
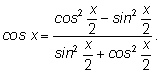 Поделим теперь числитель и знаменатель каждой дроби на
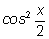 и заменим
и заменим
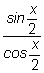 на
на
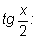
|
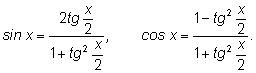
|
|
Пользуясь этими формулами, можно функцию вида
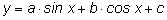 представить в виде рациональной функции от
представить в виде рациональной функции от
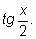 |
|
Пример.
Выразить
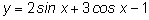 в виде функции от
в виде функции от
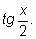
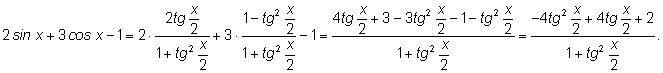
|
| |