|
Рассмотрим уравнение
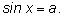 Ясно, что при
Ясно, что при
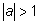 оно не имеет решений, так как синус числа
x как ордината точки
оно не имеет решений, так как синус числа
x как ордината точки
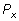 на единичной окружности по модулю не превосходит единицы. Пусть
на единичной окружности по модулю не превосходит единицы. Пусть
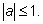 Для некоторых значений
а мы знаем хотя бы один угол
x, для которого
Для некоторых значений
а мы знаем хотя бы один угол
x, для которого
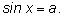 |
|
Пример.
Решить уравнение
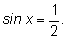
Одно решение этого уравнения
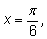 все остальные получаются по формулам
все остальные получаются по формулам
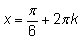 и
и
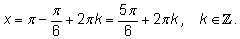
|
|
Возьмем произвольное число
а, у которого
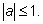 При а = +1 или а = -1 положение точки с таким значением ординаты лишь одно. Если
При а = +1 или а = -1 положение точки с таким значением ординаты лишь одно. Если 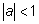 , то есть две точки на тригонометрической окружности с
данным значением синуса. Если , то есть две точки на тригонометрической окружности с
данным значением синуса. Если
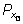 одна из них, то у точки одна из них, то у точки
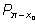 ордината будет той же самой. Всегда можно выбрать одно
решение ордината будет той же самой. Всегда можно выбрать одно
решение
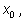 лежащее в интервале от
лежащее в интервале от
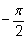 до
до
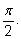 Это решение называется арксинусом числа
а.
Это решение называется арксинусом числа
а.
Обозначение:
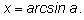
Итак, пусть
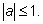 |
Арксинусом числа
а называется угол, лежащий в промежутке
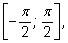 синус которого равен
а:
синус которого равен
а:
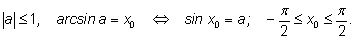
|
|
С помощью арксинуса можно записать все решения
уравнения
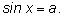 При данном значении
а (
При данном значении
а (
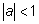 ), как мы уже отметили, есть два различных положения
точки
), как мы уже отметили, есть два различных положения
точки
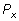 с данной ординатой. Если одному из них
соответствует
с данной ординатой. Если одному из них
соответствует
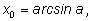 то другому – число
то другому – число
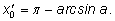 Все решения уравнения
Все решения уравнения
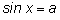 (
(
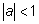 ) запишутся в виде двух бесконечных серий:
) запишутся в виде двух бесконечных серий:
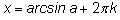 и
и
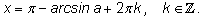
Эти две серии решений иногда описываются одной формулой:
Отметим, что при
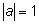 положение точки с данным значением ординаты лишь
одно. Поэтому мы исключили значения
положение точки с данным значением ординаты лишь
одно. Поэтому мы исключили значения
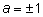 из этих формул, хотя можно записать
из этих формул, хотя можно записать
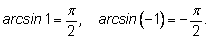
Обратим еще раз внимание на то, что
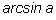 существует только в том случае, если
существует только в том случае, если
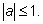
|
|
Примеры.
1)
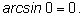
2)
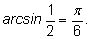
3)
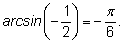
|
|
Запишем некоторые тождества для арксинуса.
1.
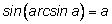
Это тождество вытекает из определения арксинуса (
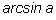 — это такой угол
х, что
— это такой угол
х, что
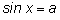 ).
).
Оно аналогично основному логарифмическому тождеству
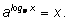
2.
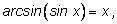 если если
если если
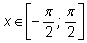
Действительно, обозначим
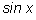 через
а. Тогда наше тождество будет равносильно
определению арксинуса:
через
а. Тогда наше тождество будет равносильно
определению арксинуса:
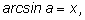 если
если
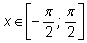 и
и
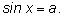
Заметим, что выражение
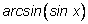 имеет смысл при любом
х, однако при
имеет смысл при любом
х, однако при
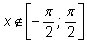 оно не равно
x.
оно не равно
x.
3.
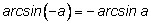
Сначала вычислим синусы от левой и правой частей. И действительно, они оказываются равными:
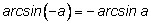 и
и
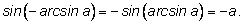
Если равны синусы двух чисел, это еще не означает, что равны и сами числа. В то же время правая часть доказываемого равенства – это угол,
принадлежащий отрезку
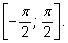 А так как левая часть тоже принадлежит этому отрезку, то левая и правая части равны между собой. А так как левая часть тоже принадлежит этому отрезку, то левая и правая части равны между собой.
|
| |