|
При
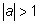 уравнение уравнение
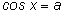 решений не имеет; если
решений не имеет; если
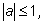 то решений уравнения бесконечно много.
то решений уравнения бесконечно много.
Если
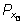 – точка на единичной окружности с абсциссой, равной
а ( – точка на единичной окружности с абсциссой, равной
а (
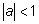 ), т. е. если
), т. е. если
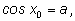 то другой точкой с этой же абсциссой будет точка
то другой точкой с этой же абсциссой будет точка
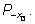 То решение уравнения
То решение уравнения
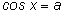 (
(
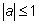 ), которое попадает в интервал от
0 до
), которое попадает в интервал от
0 до
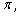 называется арккосинусом числа
а.
называется арккосинусом числа
а.
Обозначение:
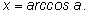
Итак, все решения уравнения
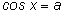 (
(
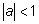 ) можно записать в виде двух серий:
) можно записать в виде двух серий:
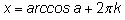 и
и
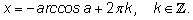 При желании обе серии можно записать более компактно:
При желании обе серии можно записать более компактно:
Как и для синуса, крайние значения
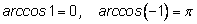 являются исключительными в том смысле, что серии
являются исключительными в том смысле, что серии
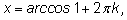 и
и
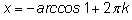 аналогично для
аналогично для
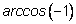 и
и
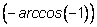 будут совпадать. Это соответствует тому, что есть только одно
положение точки
будут совпадать. Это соответствует тому, что есть только одно
положение точки
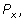 у которого абсцисса равна
1 (или
–1 ).
у которого абсцисса равна
1 (или
–1 ). |
|
Пример.
Решить уравнение
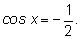
Одно решение находится легко:
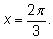 Запишем все решения так:
Запишем все решения так:
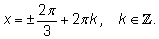
|
|
Таким образом, равенство
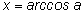 равносильно двум условиям:
равносильно двум условиям:
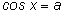 и
и
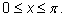 Арккосинус числа а существует лишь при
Арккосинус числа а существует лишь при
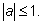
|
|
Примеры.
1)
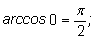
2)
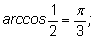
3)
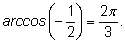
|
|
По каким причинам для значений арксинуса был выбран
отрезок
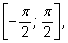 а для арккосинуса отрезок
а для арккосинуса отрезок
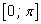 ? ?
Это объясняется тем, что на этих отрезках,
во-первых, синус и косинус принимают все возможные значения от
–1 до
1 и, во-вторых, каждое значение принимается ровно
один раз. Отрезков с этими условиями бесконечно много, но при этом
выбраны отрезки «поближе к нулю».
Для арккосинуса можно вывести ряд тождеств. |
|
1.
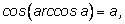 если если
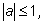 |
|
Это тождество следует из определения арккосинуса.
|
|
2.
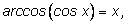 если
если
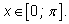 |
|
Обозначим
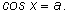 Получим определение арккосинуса:
Получим определение арккосинуса:
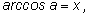 если
если
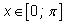 и
и
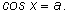
|
|
3.
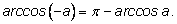 |
|
Сначала вычислим косинус от левой и правой частей:
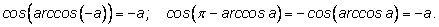
Если равны косинусы двух чисел, то это еще не означает, что равны сами
числа. Проверим, что правая часть принадлежит отрезку
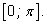 (Так как левая часть тоже принадлежит этому отрезку, то
из равенства косинусов двух чисел теперь уже будет следовать равенство
самих чисел.) Итак, надо дока¬зать, что (Так как левая часть тоже принадлежит этому отрезку, то
из равенства косинусов двух чисел теперь уже будет следовать равенство
самих чисел.) Итак, надо дока¬зать, что
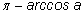 принадлежит
принадлежит
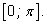 Действительно,
Действительно,
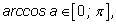
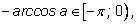
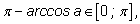 что и требовалось доказать.
что и требовалось доказать.
|
|
4.
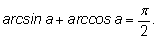
|
|
Для доказательства перепишем тождество в
равносильном виде:
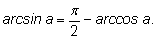
Вычислим синус от обеих частей:
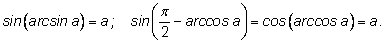
Таким образом, синусы от обеих частей равны. Отсюда
еще не следует, что равны сами эти части. Докажем, что обе они лежат в
промежутке
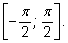 В этом промежутке синусы разных углов различны (ординаты различных
точек различны).
В этом промежутке синусы разных углов различны (ординаты различных
точек различны).
Поэтому, если синусы двух углов из этого промежутка
оказались равными, то равны и сами углы.
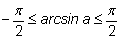 – верно по определению арксинуса. – верно по определению арксинуса.
Возьмем арккосинус.
По определению
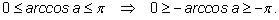 Прибавим ко всем частям по
Прибавим ко всем частям по
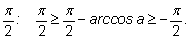 Это и есть требуемое неравенство, только записанное в другом порядке:
Это и есть требуемое неравенство, только записанное в другом порядке:
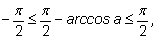 что и требовалось доказать.
что и требовалось доказать.
|
|
5.
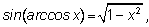
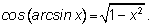 |
|
Для доказательства тождества
5 возведем его в квадрат:
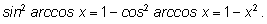 Осталось проверить знаки. Так как
Осталось проверить знаки. Так как
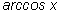 лежит в первой или второй четвертях, а синус для углов в этих
четвертях неотрицателен, то левая часть неотрицательна. Такой же знак
имеет и правая часть. Тождество доказано.
лежит в первой или второй четвертях, а синус для углов в этих
четвертях неотрицателен, то левая часть неотрицательна. Такой же знак
имеет и правая часть. Тождество доказано.
Аналогично доказывается второе тождество.
|
| |