|
Простейшие тригонометрические уравнения имеют вид
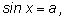
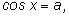
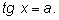 В силу периодичности тригонометрических
функций они имеют бесконечно много решений (или не имеют их вовсе).
Все решения выражаются через одно из них, и соответствующие формулы
приведены в таблице. В силу периодичности тригонометрических
функций они имеют бесконечно много решений (или не имеют их вовсе).
Все решения выражаются через одно из них, и соответствующие формулы
приведены в таблице.
|
sin x = a |
cos x = a |
tg x = a |
сtg x = a |
|
x = x0 + 2kp
x = p – x0 + 2kp |
x = ±x0 + 2kp |
x = x0 + kp |
x = x0 + kp |
Для некоторых значений
a формулы становятся проще.
|
a |
sin x = a |
cos x = a |
tg x = a |
сtg x = a |
|
0 |
x = kp |
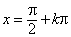 |
x = kp |
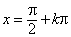 |
|
1 |
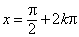 |
x = 2kp |
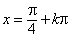 |
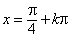 |
|
–1 |
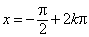 |
x = p + 2kp |
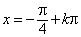 |
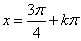 |
|
|
Замечание. Вообще для нахождения всех
решений уравнения, составленного из периодических функций с общим
периодом, надо найти все решения в пределах одного периода и затем
записать ответ в виде
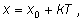 где вместо где вместо
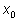 надо подставлять
найденные решения (оно может быть не одно), вместо
Т – период, а
k обозначает произвольное целое число. надо подставлять
найденные решения (оно может быть не одно), вместо
Т – период, а
k обозначает произвольное целое число. |
|
Напомним, что:
Если
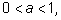 то уравнения то уравнения
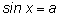 или или
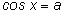 в пределах одного
периода в пределах одного
периода
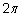 имеют два решения. Если имеют два решения. Если
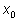 – одно из них, то для синуса в
качестве второго удобно взять
– одно из них, то для синуса в
качестве второго удобно взять
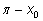 (так как (так как
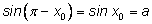 ), а для косинуса взять
), а для косинуса взять
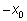 (так как (так как
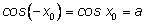 ).
).
Для тангенса ситуация упрощается, так как в пределах одного периода
тангенс принимает каждое значение (которое может быть любым
вещественным числом) ровно один раз.
Для некоторых значений
a одно из решений хорошо известно. Эти значения
а соответствуют углам
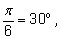
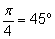 и
и
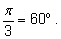
Вспомним их еще раз, записав решения соответствующих уравнений,
лежащие на промежутке
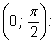
|
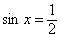 , ,
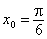 |
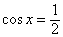 , ,
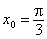 |
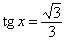 , ,
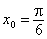 |
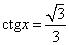 , ,
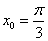 |
|
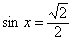 , ,
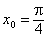 |
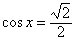 , ,
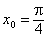 |
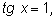
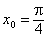 |
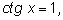
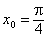 |
|
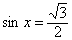 , ,
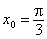 |
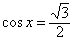 , ,
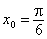 |
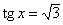 , ,
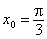 |
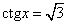 , ,
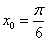 |
Заметим, что зная решение
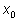 уравнения вида
уравнения вида
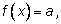 мы можем через
мы можем через
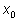 выразить одно решение уравнения
выразить одно решение уравнения
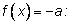
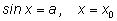
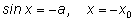
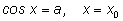
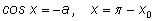
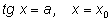
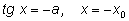
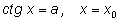
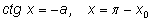
В приведенных ниже примерах в ответах везде через
k обозначено
произвольное целое число. |
|
1.
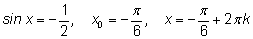 и
и
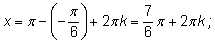
|
| |
|
2.
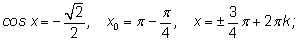
|
| |
|
3.
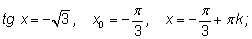
|
| |
|
4.
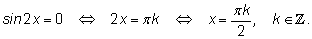
|
| |
|
5.
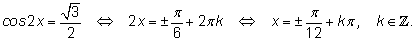
|
| |
|
6.
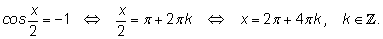
|
| |
|
7.
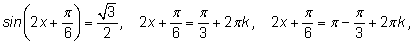
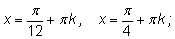
|
| |
|
8.
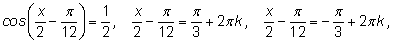
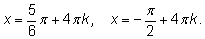
|
| |
|
9.
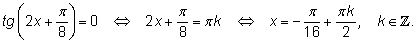
|
| |
|
10.
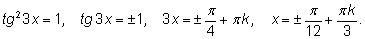
|
| |
|
11.
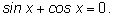 Делим на
Делим на
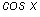 (потери корней произойти не может, так как при
(потери корней произойти не может, так как при
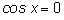 уравнение превратится в
уравнение превратится в
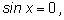 а одновременно синус и косинус в нуль не обращаются).
а одновременно синус и косинус в нуль не обращаются).
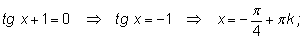
|
| |
12.
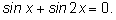 Применяем формулу синуса двойного угла.
Применяем формулу синуса двойного угла.
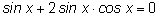
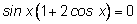
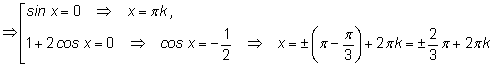
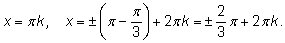
Полезно помнить, что
формулы удвоения выражают квадрат синуса или косинуса через первую
степень двойного угла:
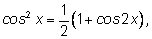
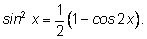
Это соображение часто
помогает понизить степень уравнения. |
| |
|
13.
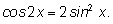 Заменяем
Заменяем
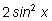 на
на
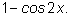 Получаем
Получаем
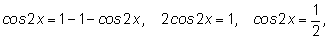
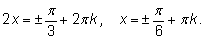 Заменять
Заменять
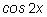 на
на
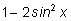 менее выгодно, так как при этом появляется уравнение
второй степени.
менее выгодно, так как при этом появляется уравнение
второй степени.
|
| |
14.
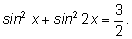 Заменяем
Заменяем
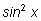 на
на
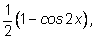 а
а
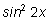 на
на
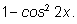
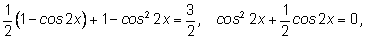
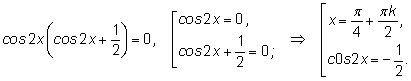
Решаем второе
уравнение:
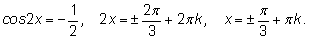 Окончательный ответ:
Окончательный ответ:
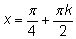 и
и
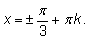
|
| |
|
15.
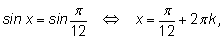
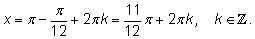
|
| |
16.
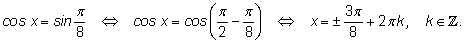
|
| |
|
17.
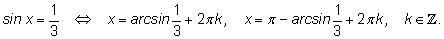
|
| |
18.
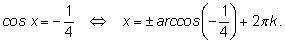
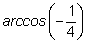 можно записать как
можно записать как
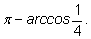
|
| |