|
Гармонические колебания – это процесс, который
может быть описан функцией вида
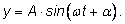 |
|
Примеры
1) Колебания упругой пружины. Конец упругой пружины (точка
P ) при ее
сжатии или растяжении описывает колебательные движения. Если на
прямой, по которой движется точка
P, ввести координату
x так, чтобы в
положении равновесия
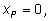 оттянуть конец пружины в положительном
направлении на расстояние
A и в момент времени
оттянуть конец пружины в положительном
направлении на расстояние
A и в момент времени
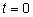 отпустить его, то
зависимость координаты точки
P от времени
t будет иметь следующий вид: отпустить его, то
зависимость координаты точки
P от времени
t будет иметь следующий вид:
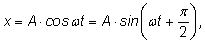 где где
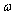 – некоторый коэффициент, характеризующий
упругость пружины. – некоторый коэффициент, характеризующий
упругость пружины.
2) Электрический колебательный контур. Рассмотрим
электрическую цепь, состоящую из последовательно соединенных
конденсатора
C и катушки индуктивности
L. Если эту цепь замкнуть
накоротко и считать, что в ней есть некоторый запас энергии (например,
ненулевой заряд в кон-денсаторе), то по этой цепи пойдет ток,
напряжение которого
U будет меняться со временем.
|
|
При идеальном предположении отсутствия потерь в
цепи зависимость
U от времени
t будет иметь следующий вид:
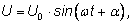 где где
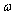 – некоторая характеристика контура, которая
вычисляется через параметры конденсатора и катушки. Константы
– некоторая характеристика контура, которая
вычисляется через параметры конденсатора и катушки. Константы
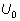 и и
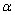 зависят от состояния цепи в данный момент времени.
зависят от состояния цепи в данный момент времени.
Таким образом, гармоническое колебание
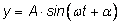 определяется
тремя параметрами: амплитудой определяется
тремя параметрами: амплитудой
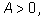 угловой скоростью угловой скоростью
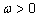 и так
называемой начальной фазой
и так
называемой начальной фазой
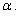 Часто вместо угловой скорости Часто вместо угловой скорости
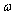 говорят
о частоте колебаний говорят
о частоте колебаний
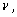 которая связана с угловой скоростью которая связана с угловой скоростью
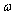 (или
иначе круговой частотой) формулой (или
иначе круговой частотой) формулой
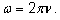 Функция
y периодична. Ее основной период равен Функция
y периодична. Ее основной период равен
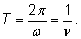 Колебания приходится складывать. В механике это связано с тем, что на
точку может действовать несколько сил, каждая из которых вызывает
гармонические колебания. В электро- и радиотехнике сложение колебаний
происходит как естественное наложение токов. Оказывается, имеет место
замечательный закон: при сложении гармонических колебаний одной и той
же частоты получается снова гармоническое колебание той же частоты. На
математическом языке это означает, что сумма двух функций
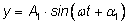 и и
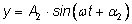 есть
функция того же вида: есть
функция того же вида:
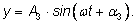
Достаточно научиться складывать функции вида
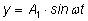 и и
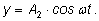 Для их сложения применяется прием введения вспомогательного
угла. Итак, рассмотрим выражение Для их сложения применяется прием введения вспомогательного
угла. Итак, рассмотрим выражение
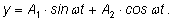 Оно похоже
на формулу синуса суммы: Оно похоже
на формулу синуса суммы:
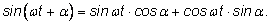 Числа
Числа
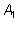 и и
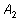 нельзя считать косинусом и синусом, однако если их
разделить на число нельзя считать косинусом и синусом, однако если их
разделить на число
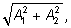 то тогда это будет возможно. Введем угол
то тогда это будет возможно. Введем угол
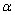 с помощью соотношений
с помощью соотношений
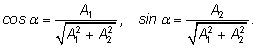 Сделаем преобразование:
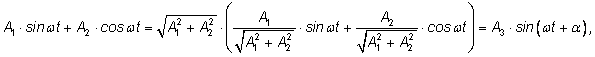 где где
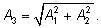
|
Пример
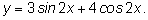 Введем вспомогательный угол Введем вспомогательный угол
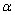 с помощью
равенств с помощью
равенств
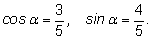 Сделаем
преобразование: Сделаем
преобразование:
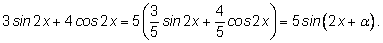
Функция
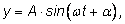 задающая гармоническое колебание, имеет период
задающая гармоническое колебание, имеет период
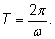 |
|
Если
T является общим периодом двух функций
f и
g,
то
T остается периодом их суммы, произведения, частного.
Сумма двух функций с различными периодами не обязательно будет
периодической. Интересен случай сложения двух функций с различными, но
очень близкими периодами. Рассмотрим, например, сумму функций
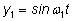 и
и
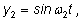 где где
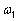 и и
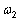 близки друг к другу. Складывая синусы,
получим близки друг к другу. Складывая синусы,
получим
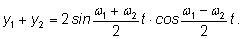 Так как Так как
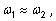 то то
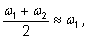 а
а
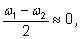 поэтому поэтому
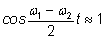 при маленьких значениях
t
и
при маленьких значениях
t
и
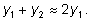 Однако с ростом
t множитель Однако с ростом
t множитель
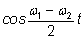 будет убывать, а затем снова возрастать, причем
изменения этого множителя значительно медленнее, чем изменения
будет убывать, а затем снова возрастать, причем
изменения этого множителя значительно медленнее, чем изменения
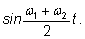
«Ровное» гармоническое колебание типа
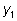 заменится «биением», график
которого изображен на рисунке. заменится «биением», график
которого изображен на рисунке.
Можно представить себе, что «биение» – это
колебание, амплитуда которого медленно (и тоже периодически) меняется.
Явление «биения» можно наблюдать при наложении звуков близкой частоты,
при измерении величины океанских приливов, которые вызываются
наложением двух периодических процессов с близкими, но различными
периодами – притяжением Солнца и притяжением Луны.
Разложение на гармоники
Чистый звуковой тон представляет собой колебание с некоторой
постоянной частотой. Музыка, которую мы слышим, представляет собой
наложение различных чистых тонов, т. е. получается сложением колебаний
с различными частотами. Преобладание звука той или иной частоты
(скажем, низких звуков или высоких) связано с амплитудой
соответствующих колебаний. Это знакомое нам разложение звуков на
чистые тона часто встречается при изучении различных колебательных
процессов.
Можно сказать так: простейшие гармонические колебания являются теми
кирпичиками, из которых складывается любое колебание. На языке
математики это означает, что любую периодическую функцию можно
представить с наперед заданной точностью как сумму синусов.
Этот замечательный факт обнаружил еще в XVIII веке Д. Бернулли при
решении задачи о колебании струны. Это показалось удивительным и
невозможным по отношению к любой функции даже такому гениальному
математику, как Л. Эйлер, который, кстати, является автором всей
современной символики тригонометрии. Систематически
разложения периодических функций в сумму синусов (или, как говорят, на
гармоники) изучал в начале XIX века французский математик Ж. Фурье.
Теперь их так и называют – разложениями (или рядами) Фурье. На рисунке
изображено приближение к периодической функции
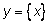 в виде суммы нескольких гармоник. Разложение
произвольного периодического сигнала на гармоники является главным
математическим аппаратом радиотехники.
в виде суммы нескольких гармоник. Разложение
произвольного периодического сигнала на гармоники является главным
математическим аппаратом радиотехники.
|
| |