|
Пусть функция
h представлена как композиция функций
f и
g, т. е.
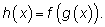 Можно обозначить Можно обозначить
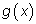 через
у, a через
у, a
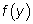 через
z. Для вычисления производной переменной
z составим
отношение через
z. Для вычисления производной переменной
z составим
отношение
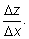 Домножив и разделив его на Домножив и разделив его на
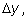 получим получим
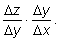 При стремлении При стремлении
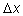 к нулю
к нулю
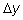 тоже
будет стремиться к нулю (принцип непрерывности). Первая дробь будет
стремиться к производной функции тоже
будет стремиться к нулю (принцип непрерывности). Первая дробь будет
стремиться к производной функции
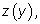 т. е. к т. е. к
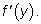 Вторая дробь будет
стремиться к производной функции Вторая дробь будет
стремиться к производной функции
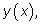 т. е. к т. е. к
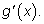 Совершая
предельный переход, получаем: Совершая
предельный переход, получаем:
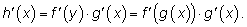
|
|
Пример.
 Вычислить производную функции Вычислить производную функции
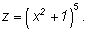 Представим
z как сложную
функцию: Представим
z как сложную
функцию:
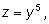 где где
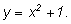 Применяя формулу производной сложной
функции, получаем: Применяя формулу производной сложной
функции, получаем:
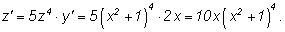
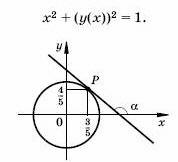
Правило дифференцирования сложной функции можно применить для
вычисления углового коэффициента касательной к кривой, заданной
уравнением. Например, рассмотрим касательную, проходящую через точку
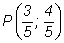 окружности окружности
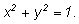
Конечно, можно выразить
у через
х и найти производную. Гораздо проще
продифференцировать уравнение окружности по переменной
х, считая
уравнение тождеством, получающимся после подстановки в него, вместо
у, его выражения через
х:
Получаем
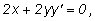 откуда откуда
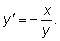 Подставляя координаты точки
Р,
получаем угловой коэффициент касательной: Подставляя координаты точки
Р,
получаем угловой коэффициент касательной:
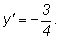
|
| |
|
Замечание. Из формулы для производной
сложной функции можно получить формулу для производной обратной
функции. Пусть функции
f
и
g взаимно обратны. Запишем тождество
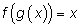 и продифференцируем его: и продифференцируем его:
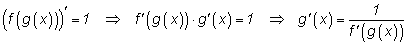
|
| |