|
1. Производная степени
Производную любой степени с натуральным показателем можно получить,
пользуясь правилом дифференцирования произведения. Например, для
нахождения производной функции
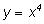 представим
представим
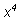 как
как
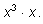 Зная производные функций
Зная производные функций
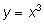 и
и
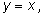 вычислим производную произведения:
вычислим производную произведения:
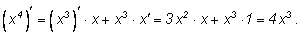
Выпишем формулы:
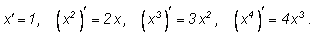
Легко заметить общую закономерность:
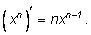
Теперь найдем производную функции : 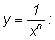
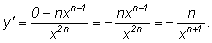
Заметим следующее: если дробь
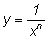 записать как
записать как
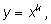 где
где
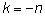 (т. е. как степень с отрицательным показателем), то
(т. е. как степень с отрицательным показателем), то
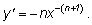
Если заменим
-n на
k, то
получим
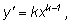 т. е. формула дифференцирования степени, полученная нами для
натуральных показателей, остается верной и для целых отрицательных
показателей:
т. е. формула дифференцирования степени, полученная нами для
натуральных показателей, остается верной и для целых отрицательных
показателей:
|
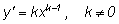 |
| Выведенная формула остается верной и для дробных
показателей. |
Возьмем известный уже нам случай
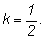 Это функция Это функция
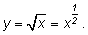
По формуле получится:
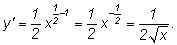
|
|
2. Производная рациональной функции
Рациональная функция задается формулой
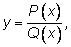 где
где
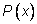 и
и
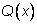 – многочлены. Производную многочлена мы найдем легко, зная
производную степени и правила дифференцирования.
– многочлены. Производную многочлена мы найдем легко, зная
производную степени и правила дифференцирования.
По правилу дифференцирования дроби получим:
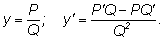
|
|
Примеры.
1)
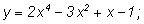
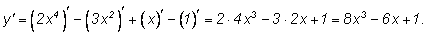
Разумеется, промежуточное равенство лишнее. Ответ можно записать
сразу.
2)
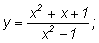
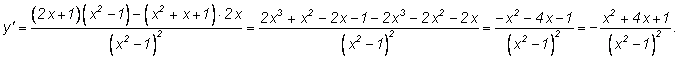
Иногда полезно перед дифференцированием дроби сделать
преобразования.
3)
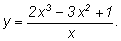
Делим почленно:
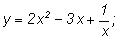
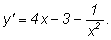
4)
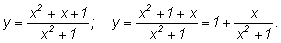
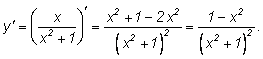
5)
 Если прямо применять формулу, то получим
Если прямо применять формулу, то получим
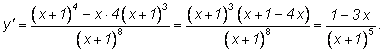
Можно поступить иначе: 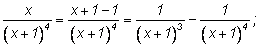
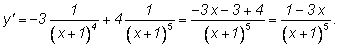
Обратите внимание на то, что если
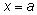 – корень знаменателя рациональной дроби кратности
k, то
– корень знаменателя рациональной дроби кратности
k, то
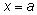 будет корнем знаменателя производной кратности, на единицу большей.
будет корнем знаменателя производной кратности, на единицу большей.
|
| |