|
1. Производная обратной функции
Выведем общую формулу производной обратной функции. Пусть
f и
g – взаимно
обратные функции. Как найти производную функции
g, зная
производную функции
f?
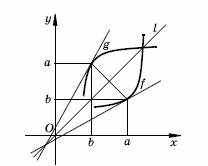 Графики
функций Графики
функций
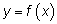 и
и
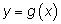 симметричны друг другу относительно биссектрисы
l угла
хОу. Возьмем
какую-нибудь точку
симметричны друг другу относительно биссектрисы
l угла
хОу. Возьмем
какую-нибудь точку
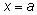 и вычислим значение одной из функций в этой точке:
и вычислим значение одной из функций в этой точке:
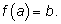 Тогда по определению обратной функции
Тогда по определению обратной функции
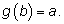
Точки
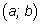 и
и
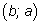 симметричны относительно указанной прямой
l. Так как
кривые симметричны, то и касательные к ним симметричны относительно
прямой
l.
симметричны относительно указанной прямой
l. Так как
кривые симметричны, то и касательные к ним симметричны относительно
прямой
l.
Из симметрии ясно, что угол одной из этих прямых с осью
х
равен углу другой прямой с осью
у. Если первая
прямая образует с осью
х угол
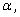 то ее угловой коэффициент равен
то ее угловой коэффициент равен
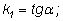 тогда вторая прямая имеет угловой коэффициент
тогда вторая прямая имеет угловой коэффициент
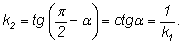
Таким образом, угловые коэффициенты прямых, симметричных
относительно прямой
l, взаимно
обратны, т .е.
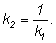
Переходя к производным и учитывая, что угловой
коэффициент касательной является значением производной в точке
касания, делаем вывод:
|
Значения производных взаимно обратных функций в соответствующих
точках взаимно обратны, т. е.
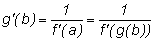
|
|
Замечание. В приведенных выше рассуждениях
предполагалось, что
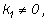 т. е. касательные к кривым не параллельны осям координат.
т. е. касательные к кривым не параллельны осям координат.
|
|
Примеры.
1)
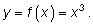 Обратной функцией будет функция
Обратной функцией будет функция
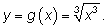 Найдем производную функции
g:
Найдем производную функции
g:
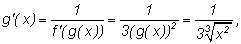 т.е.
т.е.
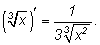
Аналогично можно вывести формулу производной функции
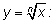
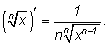
2) Пусть
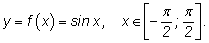
Обратной функцией будет
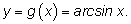
Найдем производную арксинуса:
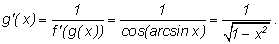
Итак,
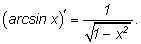
Аналогично вычисляется производная арктангенса:
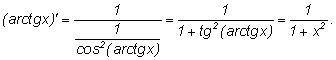 т.е.
т.е.
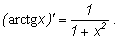
|
| |