Математика изучает различные связи между величинами. Важнейшие примеры таких связей дает механическое движение. Мы уже знаем, что между положением (координатой) то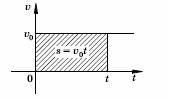чки и ее скоростью есть известная связь, лежащая в основе математического анализа: скорость является производной от координаты по времени. Сама операция нахождения производной называется дифференцированием. Обратная задача – нахождение положения точки по ее скорости – решается с помощью другой математической операции, называемой интегрированием.
Мы знаем много примеров пар величин, которые связаны между собой так же, как положение точки и ее скорость. Нахождение одной из этих величин, если известна другая, мы свели к операции дифференцирования. Например, линейная плотность тонкого стержня есть производная его массы по длине, мощность есть производная работы по времени, сила тока есть производная заряда по времени и т. д. С помощью обратной операции – интег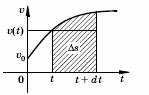рирования мы сможем вычислять массу по заданной плотности, работу по известной мощности, заряд по заданной силе тока и т. д.
Прежде чем учиться вычислять интегралы, рассмотрим их геометрический смысл. Начнем с задачи о механическом движении. Пусть точка движется с постоянной скоростью 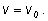   Графиком скорости в системе координат 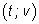   будет прямая 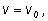   параллельная оси времени  t.  Если считать, что в начальный момент времени 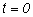   точка находилась в начале координат, то путь ее  s,  пройденный за время  t,  вычисляется по формуле 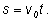   Величина 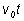   представляет собой площадь прямоугольника, ограниченного графиком скорости, осью абсцисс и двумя вертикальными прямыми, т. е. путь точки можно вычислить как площадь под графиком скорости.
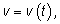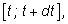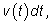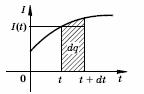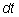Обратимся к случаю неравномерного движения. Теперь скорость можно считать постоянной только на маленьком отрезке времени. Если скорость  v  меняется по закону    то путь, пройденный за отрезок времени    приближенно выразится произведением    а на графике – площадью прямоугольника со сторонами    и 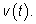   Точное значение пути за отрезок времени 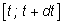   равно площади криволинейной трапеции, закрашенной на рисунке. Весь путь получится сложением площадей таких криволинейных трапеций, т. е. выразится как площадь под графиком скорости.
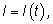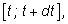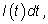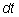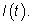Аналогично если мы начертим график зависимости силы тока от времени    то величина заряда  q,  перенесенного током за отрезок времени    приближенно можно вычислить по формуле    т. е. представить площадью прямоугольника со сторонами    и    Точную величину заряда можно вычислить как площадь под графиком силы тока. Таким образом, задача интегрирования тесно связана с задачей вычисления площади.