|
«Метод исчерпывания» Архимеда хотя и не дал
общего способа вычисления площади, однако сыграл очень большую роль
в математике, так как с его помощью удалось объединить самые разные
задачи – вычисление площади, объема, массы, работы, давления,
электрического заряда, светового потока и многие, многие другие.
Проиллюстрируем этот метод на простом примере. Предположим, что нам
надо вычислить объем лимона, имеющего неправильную форму, и поэтому
применить какую-либо известную формулу объема нельзя. С помощью
взвешивания найти объем также трудно, так как плотность лимона в
разных частях его разная. Поступим следующим образом. Разрежем лимон
на тонкие дольки.
Каждую дольку приближенно можно считать цилиндром, радиус основания
которого можно измерить. Объем такого цилиндра вычислить легко по
готовой формуле. Сложив объемы маленьких цилиндров, мы получим
приближенное значение объема всего лимона. Приближение будет тем
точнее, чем на более тонкие части мы сможем разрезать лимон.
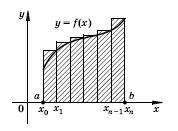 Применим
аналогичную процедуру для вычисления площади подграфика. Рассмотрим
подграфик функции
f, заданной
на отрезке Применим
аналогичную процедуру для вычисления площади подграфика. Рассмотрим
подграфик функции
f, заданной
на отрезке
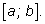 Разобьем этот отрезок на несколько частей. Площадь всего подграфика
разобьется на сумму площадей более мелких криволинейных трапеций.
Каждую такую трапецию можно приближенно считать прямоугольником.
Сумма площадей этих прямоугольников дает приближенное представление
о всей площади подграфика. Чем мельче мы разобьем отрезок
Разобьем этот отрезок на несколько частей. Площадь всего подграфика
разобьется на сумму площадей более мелких криволинейных трапеций.
Каждую такую трапецию можно приближенно считать прямоугольником.
Сумма площадей этих прямоугольников дает приближенное представление
о всей площади подграфика. Чем мельче мы разобьем отрезок
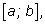 тем точнее вычислим площадь. Запишем проведенное рассуждение с
помощью формул.
тем точнее вычислим площадь. Запишем проведенное рассуждение с
помощью формул.
Разделим отрезок
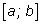 на
n частей
точками
на
n частей
точками
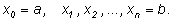 Длину
k–го отрезка
обозначим через
Длину
k–го отрезка
обозначим через
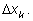 Составим сумму
Составим сумму
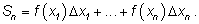
Геометрически эта сумма представляет собой площадь закрашенной
ступенчатой фигуры. Суммы вида
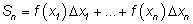 называются интегральными суммами для функции
f.
называются интегральными суммами для функции
f.
Интегральные суммы дают приближенное значение площади. Точное
значение получается при помощи предельного перехода. Представим
себе, что мы измельчаем разбиение отрезка
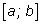 так, что длины всех маленьких отрезков стремятся к нулю (т. е.
так, что длины всех маленьких отрезков стремятся к нулю (т. е.
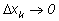 ). Тогда площадь ступенчатой фигуры будет приближаться к
площади подграфика
S. Можно сказать, что площадь подграфика равна
пределу интегральных сумм, т. е.
). Тогда площадь ступенчатой фигуры будет приближаться к
площади подграфика
S. Можно сказать, что площадь подграфика равна
пределу интегральных сумм, т. е.
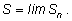
Тем самым и про интеграл можно сказать так:
|
|
Интеграл равен пределу интегральных сумм. |
|
С помощью интегральных сумм можно приближенно
вычислять самые различные величины. |
|
Примеры.
1) Объем лимона. Обозначим толщину
k-й дольки через
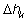 (необязательно резать лимон на дольки одинаковой
толщины), а радиус ее через
(необязательно резать лимон на дольки одинаковой
толщины), а радиус ее через
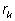 (
( 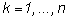 – это означает, что мы разрезали лимон на
n долек). Объем
лимона приближенно представим интегральной суммой
– это означает, что мы разрезали лимон на
n долек). Объем
лимона приближенно представим интегральной суммой
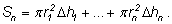
|
| |
|
2) Работа. Предположим, что на
точку, движущуюся по оси
х, действует
некоторая сила
F, направленная
по той же оси. Мы знаем, что если сила
F постоянна, то
работа равна
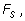 где
s – путь, пройденный
точкой. Предположим теперь, что
F меняется от
точки к точке и нам известно ее значение
где
s – путь, пройденный
точкой. Предположим теперь, что
F меняется от
точки к точке и нам известно ее значение
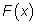 в каждой точке
х
некоторого промежутка
в каждой точке
х
некоторого промежутка 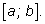 Как найти работу
A по
перемещению точки из
а в
b?
Как найти работу
A по
перемещению точки из
а в
b?
Разобьем отрезок
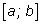 на
n отрезков.
Будем приближенно считать, что на каждом отрезке сила постоянна. В
качестве постоянной силы на отрезке
на
n отрезков.
Будем приближенно считать, что на каждом отрезке сила постоянна. В
качестве постоянной силы на отрезке
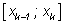 можно взять значение функции
F в одной из
точек этого отрезка, например в точке
можно взять значение функции
F в одной из
точек этого отрезка, например в точке
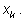 Работу на
k-м отрезке пути
приближенно можно представить как произведение
Работу на
k-м отрезке пути
приближенно можно представить как произведение
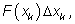 а на всем отрезке – интегральной суммой:
а на всем отрезке – интегральной суммой:
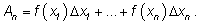
Точное значение работы
А получается
предельным переходом:
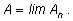
Вычисление пределов интегральных сумм оказалось очень трудным. Даже
для простейших функций этот способ вычисления интегралов сложен.
Архимед сумел вычислить некоторые площади, объемы, фактически находя
пределы интегральных сумм для квадратичной функции. Однако этот
результат стоял особняком в математике до конца XVII в., когда
выяснилось, что задача нахождения площади является обратной к задаче
нахождения скорости.
|
| |