Изображение на весь экран - нажать клавишу F11
 
Скорость роста площади
 

Рассмот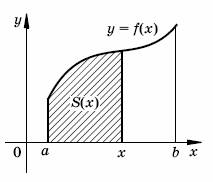рим положительную функцию  f,  заданную на отрезке    Представим себе «переменную» криволинейную трапецию, полученную следующим образом: закрепим левую стенку 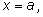   а правую начнем двигать вдоль оси абсцисс. Такая трапеция изображена на рисунке закрашенной фигурой. Ее можно считать подграфиком функции  f,  область определения которой ограничена отрезком  
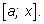
Обозначая площадь криволинейной трапеции, т. е. площадь подграфика функции  f,  заданной на отрезке 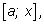   через 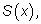   получим новую функцию 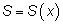   (переменная площадь). Перечислим свойства функции  S.  Она определена для всех 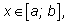   ее значение при 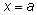   равно нулю (трапеция вырождается в отрезок, и ее площадь равна нулю), эта функция возрастает, и при 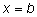   ее значение равно площади всего подграфика, т. е. интегралу от функции  f.
Найдем скорость роста функции  S  и результат запишем в виде теоремы.
 

Теорема (о скорости роста площади).
Пусть  f – положительная функция,  S – переменная площадь ее подграфика. Тогда производная функции  S  равна функции  f,  т. е.


 

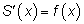
Итак, теорема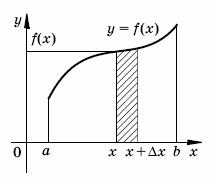 утверждает, что производная переменной площади подграфика функции  f  равна самой функции  f.  Для доказательства теоремы поступим так, как всегда поступают при вычислении производной. Зафиксируем значение аргумента  х  и дадим аргументу приращение 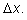   Вычислим приращение функции: 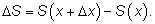   На рисунке видно, что приращение площади есть площадь подграфика функции  f,  определенной на отрезке  
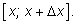
Если 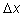   достаточно мало, то площадь заштрихованной на рисунке криволинейной трапеции мало отличается от площади прямоугольника со сторонам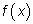и    и 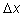   т. е. можно записать приближенное равенство  
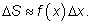
Отсюда мы делаем вывод, что 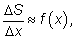   т. е. производная функции  S  равна функции  f,  что и утверждалось в теореме.

Замечание. В доказательстве теоремы мы использовали такое соображение: если отрезок 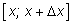   достаточно мал, то площадь подграфика функции  f  на этом отрезке мало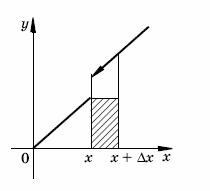 отличается от произведения 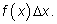   Но если в точке  х  функция  f  имеет разрыв, то это неверно, что хорошо видно на рисунке. Поэтому в формулировку теоремы о скорости роста площади надо добавить требование непрерывности функции  f.
Подведем итог. Для функции  f  мы построили новую функцию  S – переменную площадь подграфика. Связь между функциями  f  и  S  такова:  S – интеграл от функции  f,  f – производная функции  S.
Из этого видно, что нахождение интеграла (интегрирование) и нахождение производной (дифференцирование) являются взаимно обратными операциями. Если мы знаем функцию  f,  то нахождение функции  S  (площади подграфика функции  f) есть задача интегрирования функции  f.  Если же задана функция  S,  то нахождение функции  f  (скорости роста площади) есть задача дифференцирования функции  S.
 
 
<< назад               вперед >>
В оглавление модулей / В расписание уроков