| 1. Определение предела
последовательности |
|
Определение. Число
А
называется пределом последовательности
a1,
a2, …, если, начиная с
некоторого места, все члены этой последовательности будут сколь
угодно мало отличаться от
А.
Обозначение:
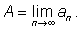 |
|
Примеры. Вычислим пределы некоторых последовательностей.
1.
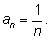
Ясно, что пределом этой последовательности будет число
0.
Действительно, взяв произвольное число 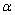 > 0,
мы можем найти такой номер последовательности, после которого каждый
член
an
будет меньше > 0,
мы можем найти такой номер последовательности, после которого каждый
член
an
будет меньше
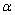 (т. е.
(т. е.
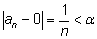 ).
Действительно, ).
Действительно,
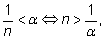 так что достаточно взять любое
n,
большее числа
так что достаточно взять любое
n,
большее числа
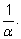 Итак,
Итак,
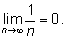
2.
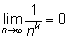 при любом
k > 0.
Действительно, мы можем решить неравенство
при любом
k > 0.
Действительно, мы можем решить неравенство
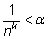 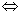 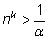
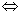
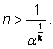
Справа стоит вполне конкретное положительное число, которое
указывает нам, с какого места число
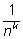 станет меньше наперед заданного числа
станет меньше наперед заданного числа
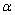 > 0.
> 0.
3.
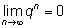 при
|q| < 1.
при
|q| < 1.
Решить неравенство
|q|n
<
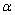 не просто – для этого нужны логарифмы.
не просто – для этого нужны логарифмы.
Запишем это решение:
|q|n
<
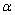
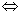 n lg |q| < lg
n lg |q| < lg
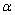
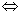
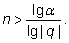
Знак неравенства поменяется, потому что
lg |q| < 0
при
|q| < 1.
Отрицательным будет и
lg
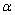 ,
если ,
если
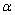 < 1,
и мы получим положительную границу для
n. < 1,
и мы получим положительную границу для
n.
Однако нам не обязательно находить самое первое значение номера
n,
начиная с которого число
|q|n
станет меньше данного числа
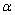 . .
Достаточно дать оценку для степени
|q|n.
Это можно сделать, например, с помощью неравенства Бернулли:
(1 + a)n
> 1 + na,
верного при любом
a > 0.
Возьмем
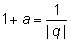 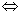 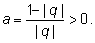 Получим
Получим
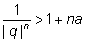 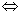 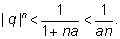
Ясно, что дробь
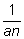 (a
> 0)
может быть сделана сколь угодно малой. (a
> 0)
может быть сделана сколь угодно малой.
|
| 2. Существование предела
Рассмотрим такое число
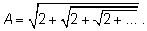 Что такая запись может обозначать? Можно начать с числа
Что такая запись может обозначать? Можно начать с числа
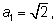 затем перейти к числу
затем перейти к числу
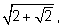 затем под последним корнем прибавить
затем под последним корнем прибавить
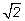 и так «продолжать до бесконечности». Мы столкнулись с
последовательностью
a1,
a2, …,
у которой
и так «продолжать до бесконечности». Мы столкнулись с
последовательностью
a1,
a2, …,
у которой
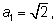 а каждый следующий вычисляется по рекуррентной формуле
а каждый следующий вычисляется по рекуррентной формуле
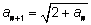 или
или
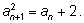 Интересующее нас число надо понимать как предел последовательности
(an),
т. е.
Интересующее нас число надо понимать как предел последовательности
(an),
т. е. 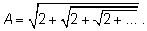 = =
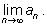
Чему же равно число
А
и существует ли оно? «Перейдем в равенстве
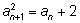 к пределу» (чуть позже разберемся в смысле этих слов).
Получим
А2 =
А + 2,
или
А2 –
А – 2 = 0, откуда
А = 2
или
А = –1.
Так как, судя по записи с радикалами,
A > 0,
то выберем значение
А = 2,
т. е.
к пределу» (чуть позже разберемся в смысле этих слов).
Получим
А2 =
А + 2,
или
А2 –
А – 2 = 0, откуда
А = 2
или
А = –1.
Так как, судя по записи с радикалами,
A > 0,
то выберем значение
А = 2,
т. е.
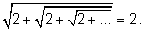
Начнем с переходов к пределу. Они основаны на упоминавшихся ранее
правилах перехода к пределу при арифметических действиях с
последовательностями.
Равенство
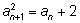 можно понимать как арифметическую связь между последовательностями:
последовательность
bn =
an + 1 – это та же
последовательность
(an),
только начинающаяся со второго ее члена, число
2
можно понимать как «постоянную последовательность»
cn,
где
cn
= 2 при всех
n.
Теперь рекуррентное соотношение запишем как
bn
можно понимать как арифметическую связь между последовательностями:
последовательность
bn =
an + 1 – это та же
последовательность
(an),
только начинающаяся со второго ее члена, число
2
можно понимать как «постоянную последовательность»
cn,
где
cn
= 2 при всех
n.
Теперь рекуррентное соотношение запишем как
bn bn = an + cn.
Применяя правило перехода к пределу, получим
А2
= А + 2.
При этом использованы два очевидных соображения:
пределы последовательностей
an
и
bn =
an + 1 равны между собой, а
предел постоянной последовательности равен значению каждого ее члена. bn = an + cn.
Применяя правило перехода к пределу, получим
А2
= А + 2.
При этом использованы два очевидных соображения:
пределы последовательностей
an
и
bn =
an + 1 равны между собой, а
предел постоянной последовательности равен значению каждого ее члена.
Казалось бы все обосновано, и задача решена. Применим метод решения
к последовательности, заданной рекуррентным соотношением
an + 1
= 2an – 1. Обозначим
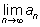 через
А
и перейдем к пределу:
А = 2А –
1
через
А
и перейдем к пределу:
А = 2А –
1
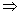 А = 1.
Действительно, если возьмем
a1
= 1,
то получим, что
а2
= 2
А = 1.
Действительно, если возьмем
a1
= 1,
то получим, что
а2
= 2 1 – 1 = 1,
а3
= 1 и т. д., т. е. 1 – 1 = 1,
а3
= 1 и т. д., т. е.
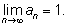 Однако, если мы начнем с
а1
= 2,
то получим последовательность
2, 3,
5, 9, 17, …,
общий член которой легко угадывается
an =
n2 + 1
(и легко проверяется по индукции), но никакого предела
у последовательности
an
= n2 + 1 быть не может. Наша
ошибка состоит в том, что сформулированные (без доказательства)
правила обращения с пределами предполагают существование
пределов всех существующих последовательностей.
Однако, если мы начнем с
а1
= 2,
то получим последовательность
2, 3,
5, 9, 17, …,
общий член которой легко угадывается
an =
n2 + 1
(и легко проверяется по индукции), но никакого предела
у последовательности
an
= n2 + 1 быть не может. Наша
ошибка состоит в том, что сформулированные (без доказательства)
правила обращения с пределами предполагают существование
пределов всех существующих последовательностей.
Понятно, что одни последовательности имеют пределы (сходящиеся
последовательности), другие – нет (расходящиеся
последовательности). |
|
|
Нахождение
корней квадратного уравнения
Калькулятор выполнен в виде Java-скрипта.
Находится в коллекции свободного доступа и может быть включен в
HTML-страницу простым копированием.
This free script provided by JavaScript Kit
|
|
|
Упражнение.
Используя инструменты, выполните следующие задания.
1. Найдите значение выражения
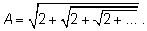 экспериментально как предел рекуррентно заданной последовательности.
экспериментально как предел рекуррентно заданной последовательности.
2. Найдите значение выражения
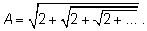 как
корень квадратного уравнения.
как
корень квадратного уравнения. 3. Найдите
экспериментально предел рекуррентно заданной последовательности
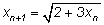 для разных начальных значений
x0.
для разных начальных значений
x0.
4. Найдите предел рекуррентно
заданной последовательности
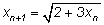 как корень квадратного уравнения.
как корень квадратного уравнения.
5. Найдите рекуррентно заданную
последовательность, предел которой совпадает с одним из корней
уравнения x2
- 3x - 1. |
| |